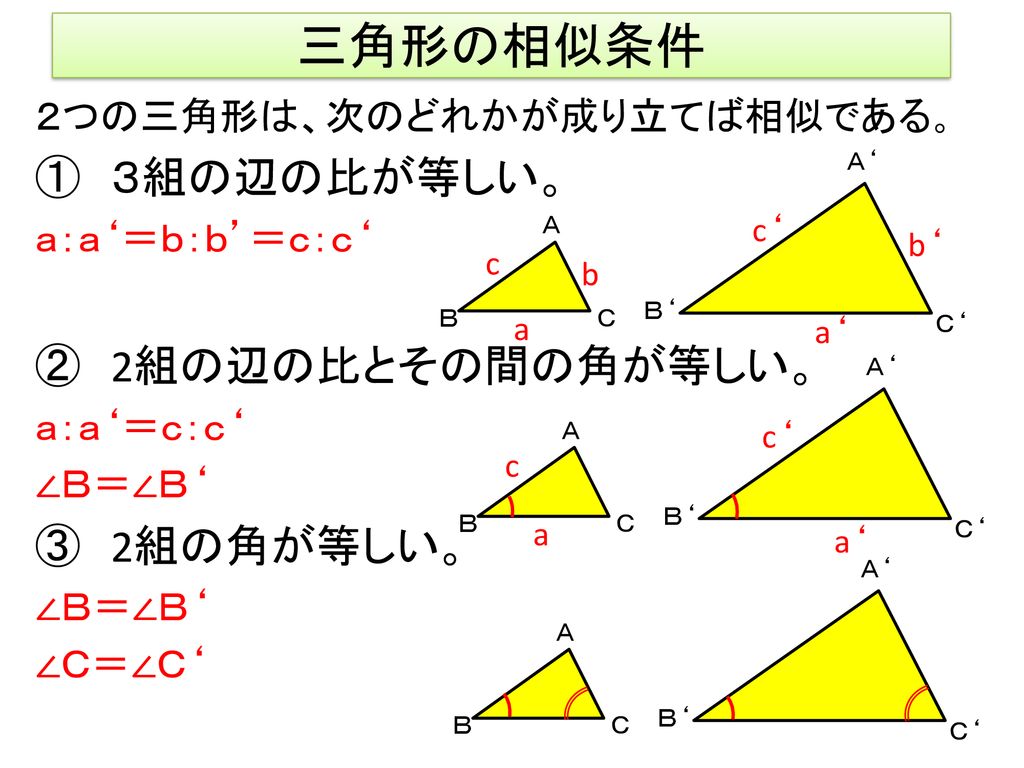
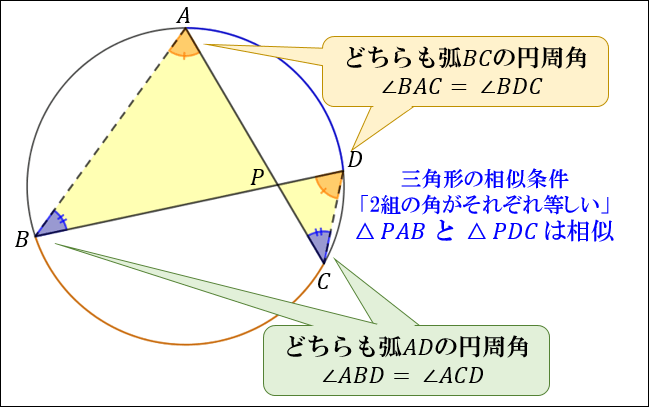
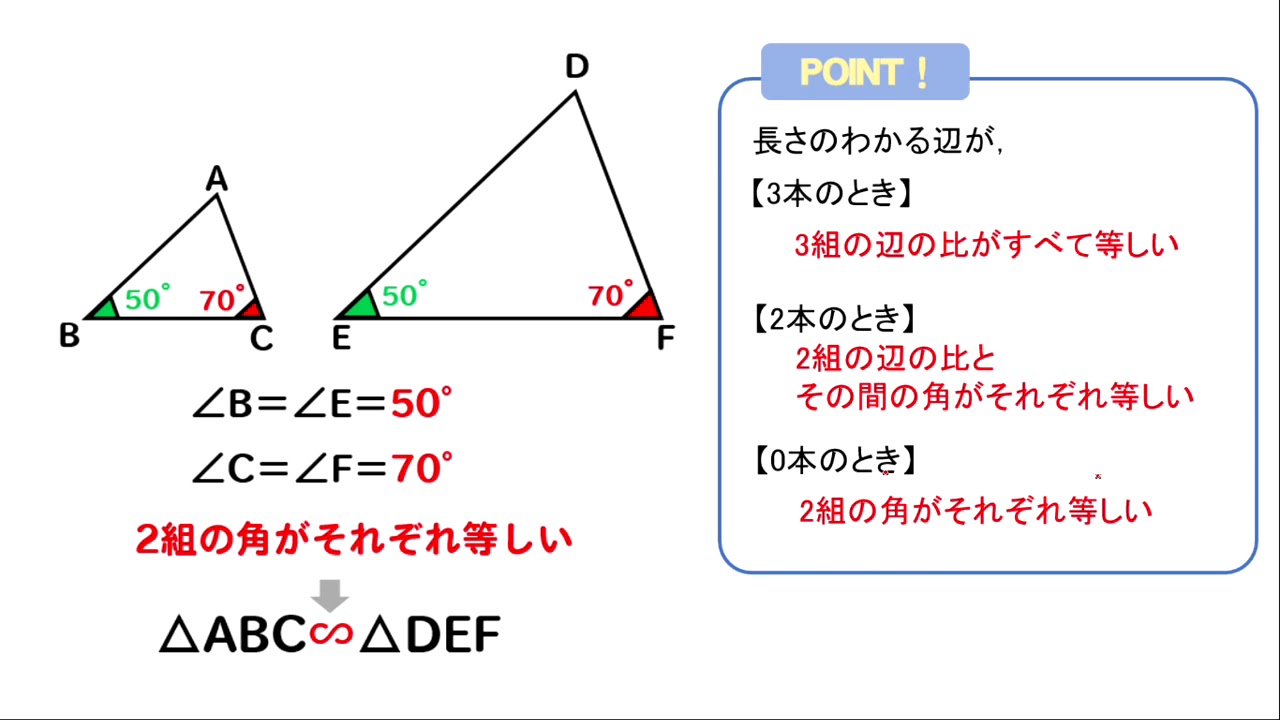
三角形の相似条件 相似の問題の中でも、三角形の相似を証明する問題が多く出題されます。 ここでは、三角形の相似を証明するために必要な3つの条件を説明します。 私が実際に問題を解いた時に使う回数が多いと感じた順に書いてみました。 1つめは
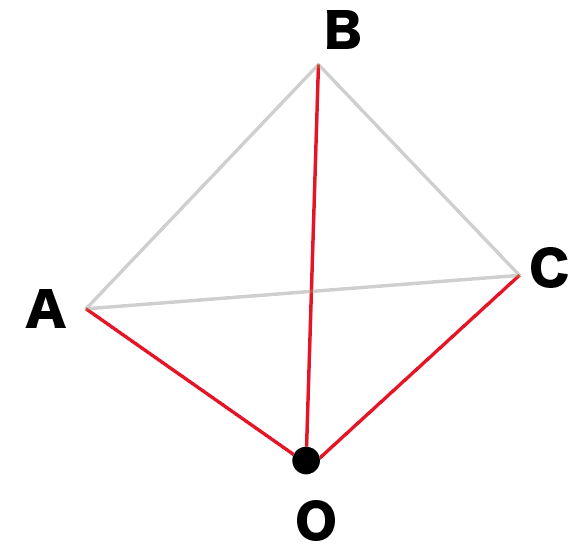
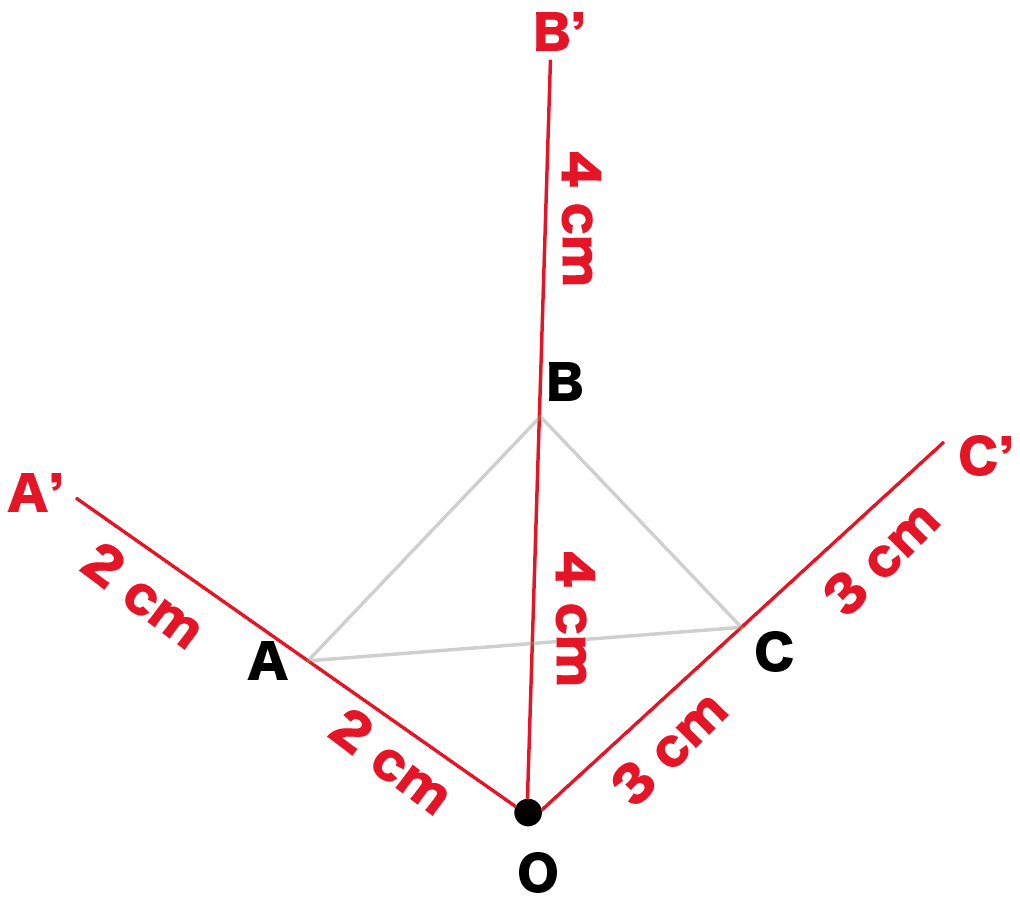
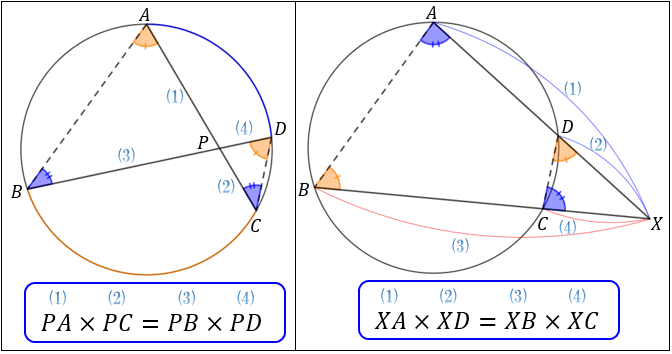
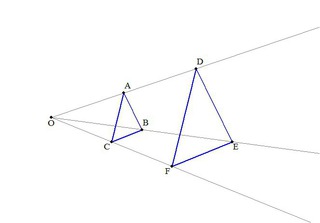
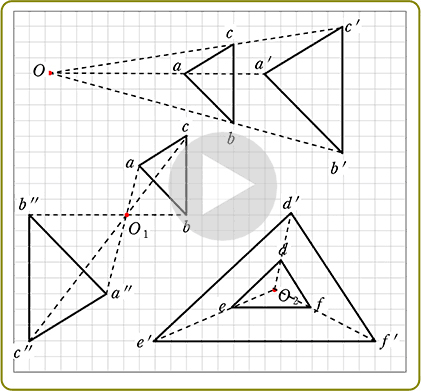
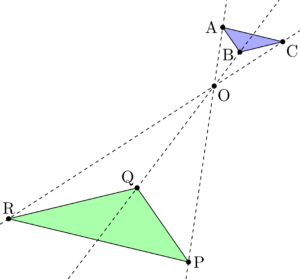
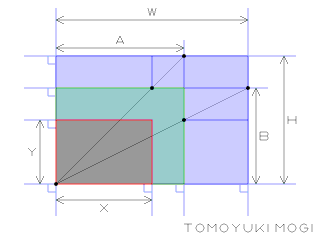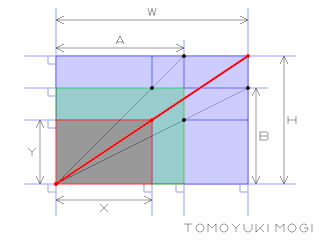
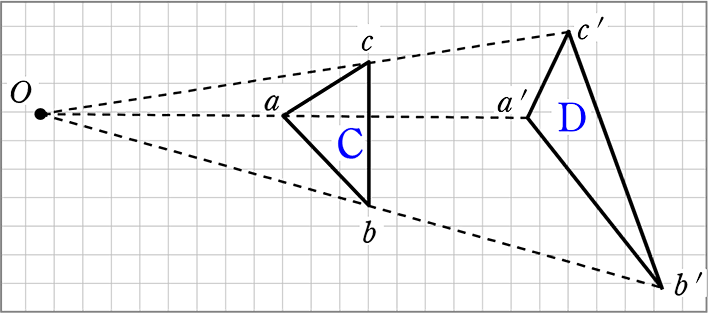
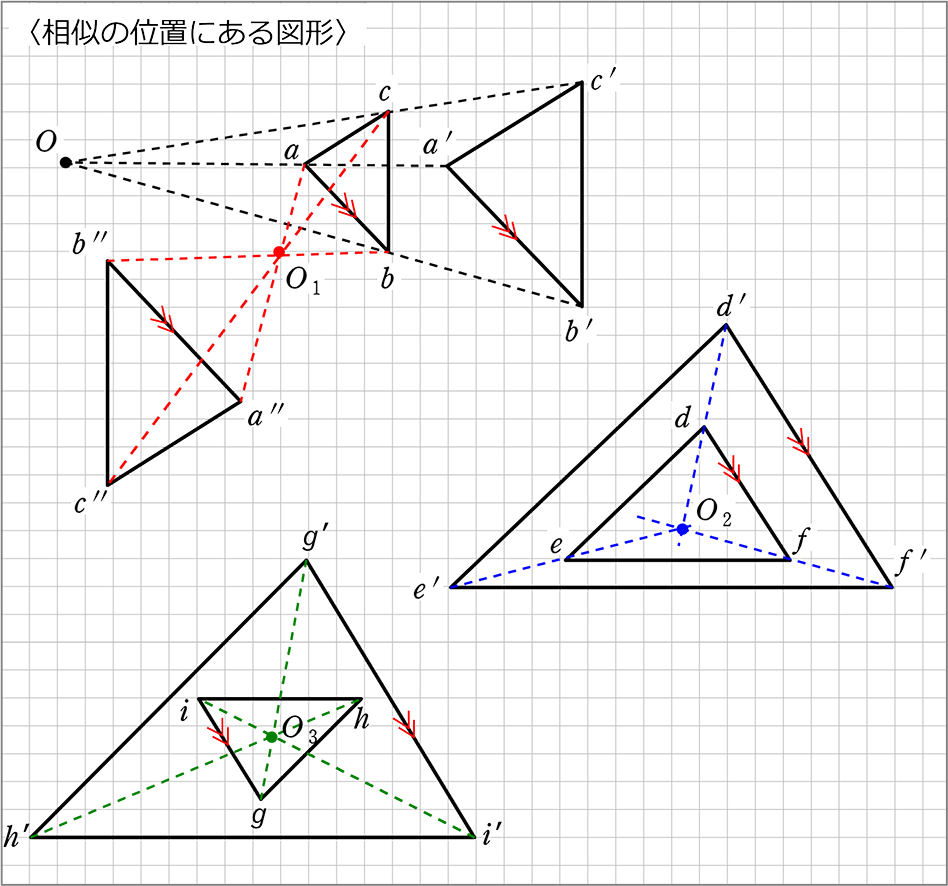
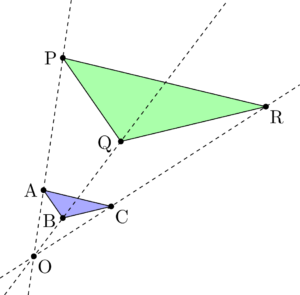
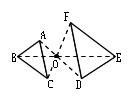
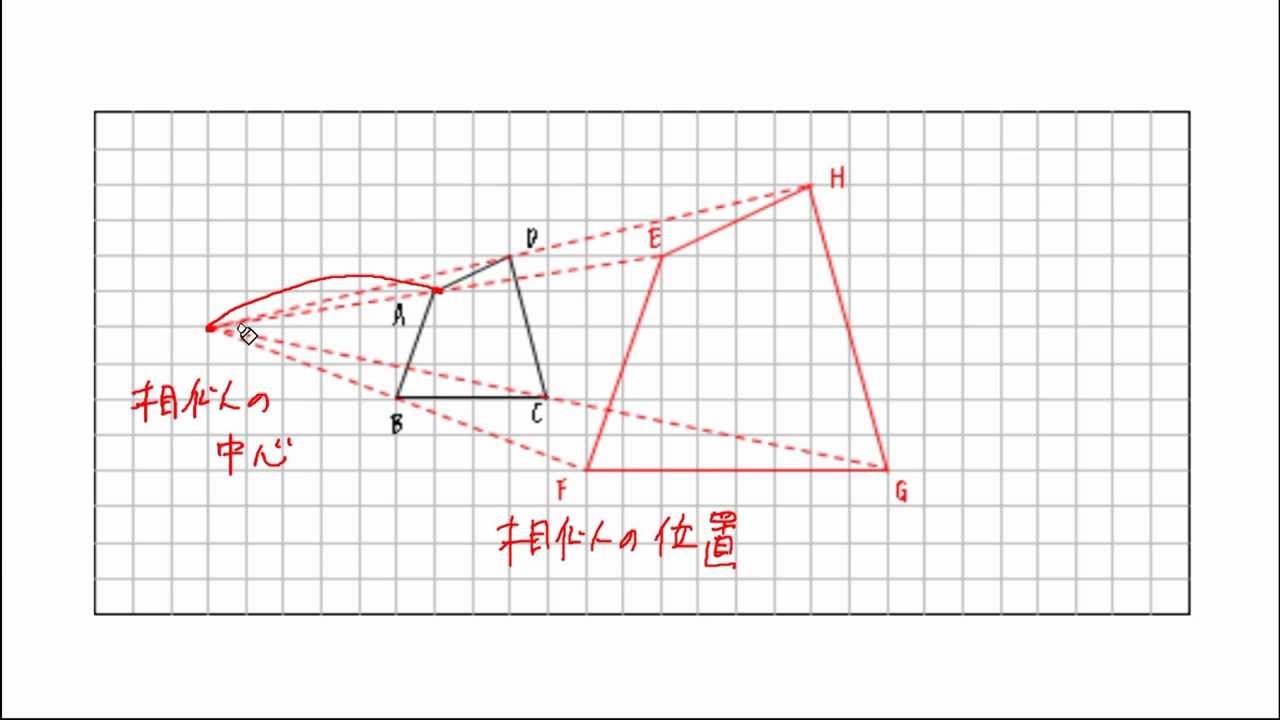
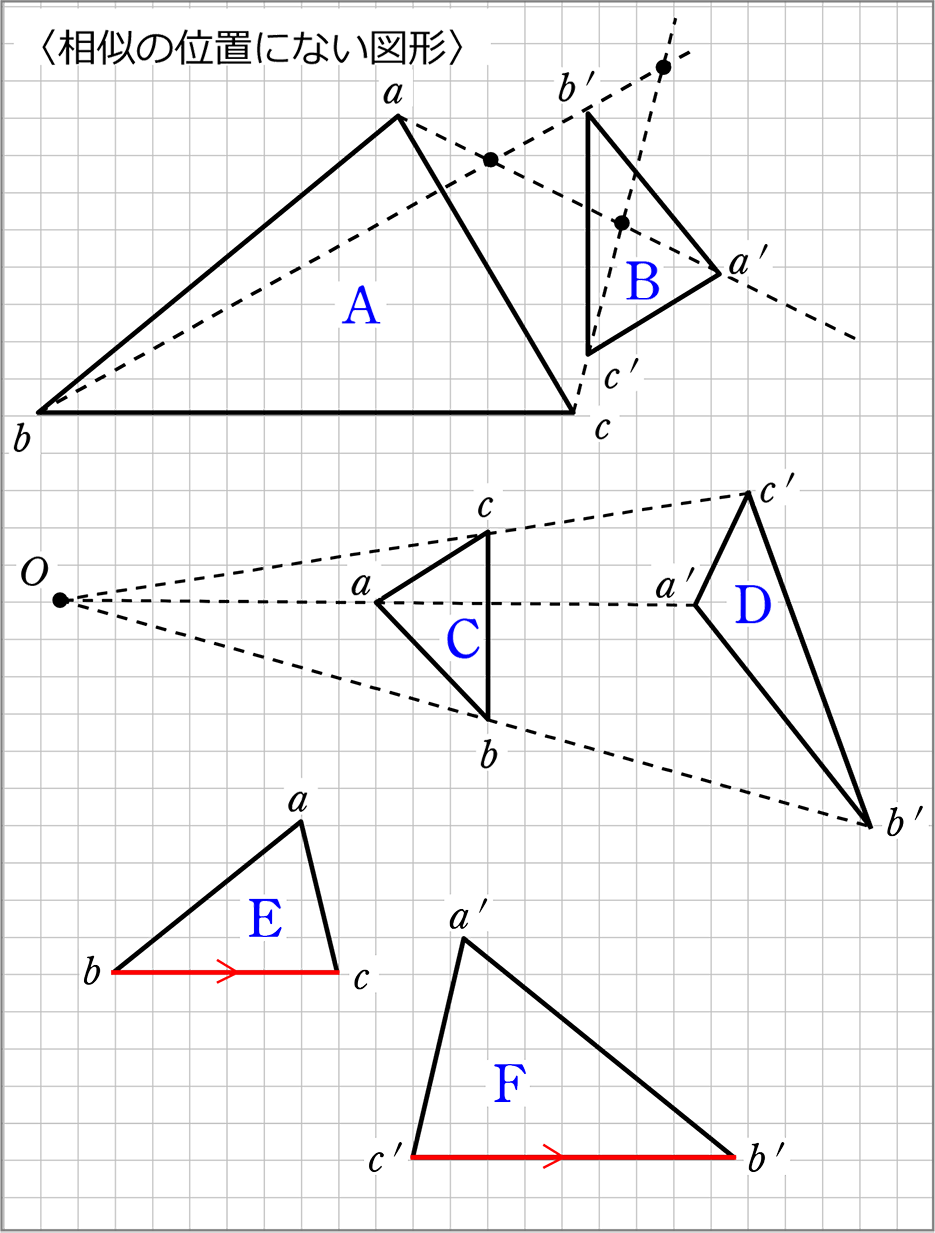
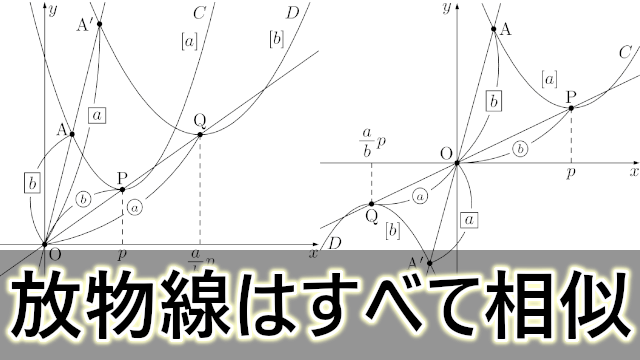
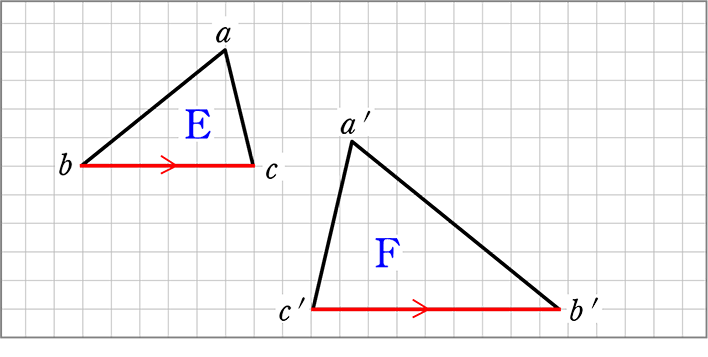
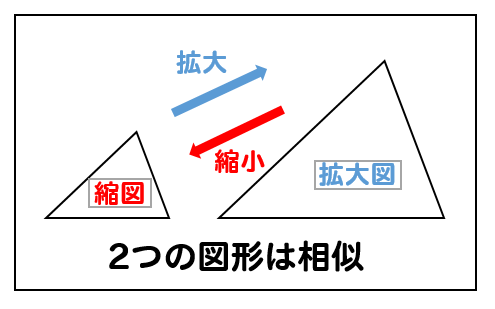
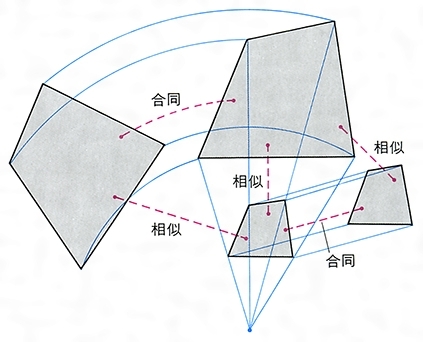
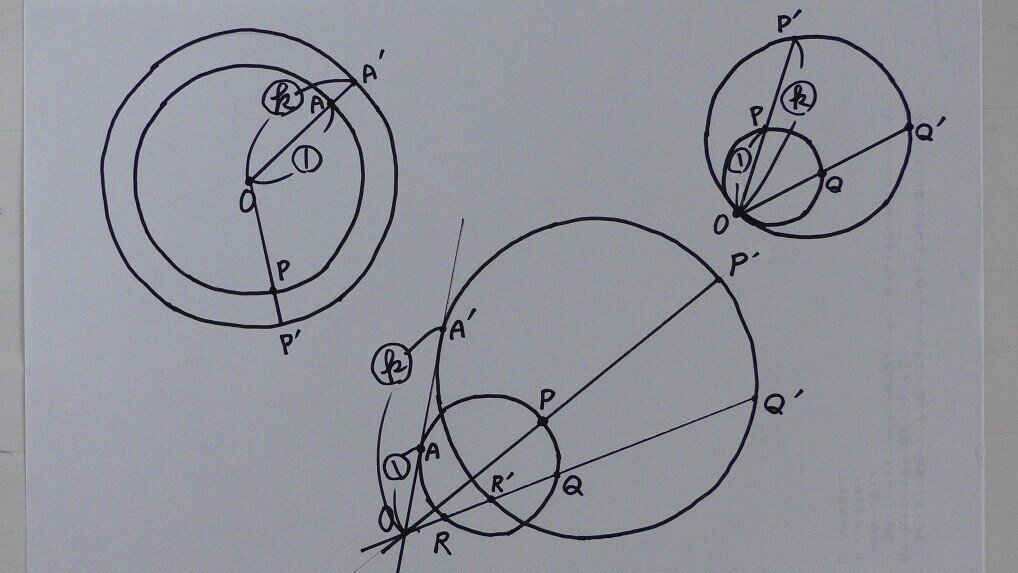
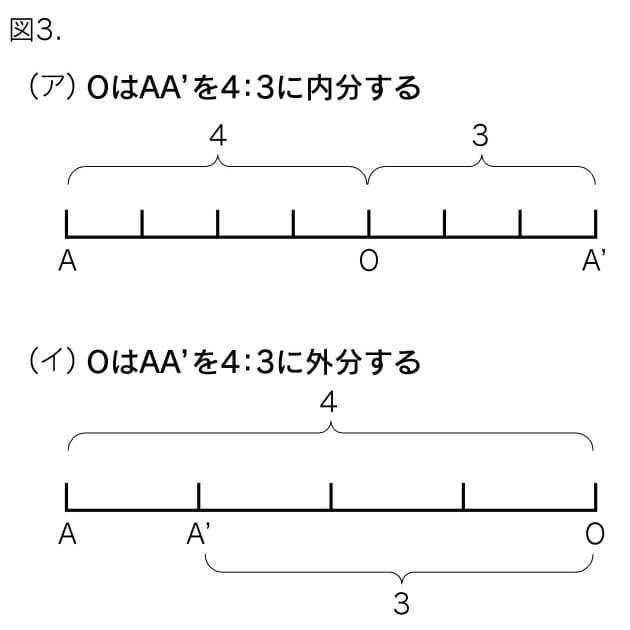
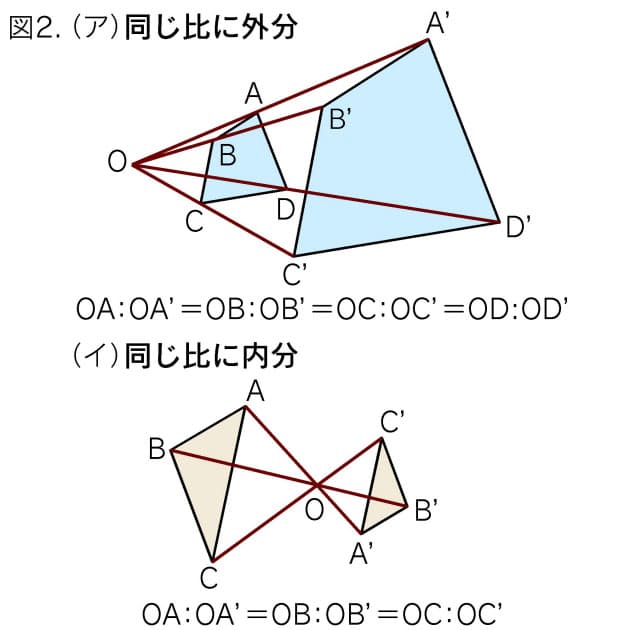
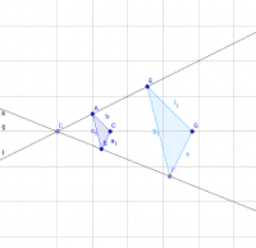
相似の中心 定義-上図の場合、\(abde=bcef=cafd=12\) より、相似となります。 条件② 2組の辺の比とその間の角がそれぞれ等しい 2組の辺の比が等しく、その間の角も等しいとき「それらの三角形は相似である」ということができます。相似の学習における定義の問題点は,以前から指摘されている. 4 の p71 には,『相似 にも種々の定義がある.たとえば相似形は「形が全く同じ図形」,「同じ割合で拡大縮小す れば重なる図形」,「相似の位置におくことができる図形」などさまざまなものが用いられ る.しかし,これらには,それぞれ長所・短所がある.第1の定義は,一見わかりよく算 いかえただけで真の定義になって
相似の中心 定義のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  |  |
 |  |  |
 |  | |
「相似の中心 定義」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  | |
 | ||
「相似の中心 定義」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  | |
 |  |  |
「相似の中心 定義」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
 |  | |
「相似の中心 定義」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  |  |
「相似の中心 定義」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「相似の中心 定義」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
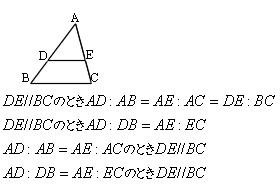 | ||
 |  | |
 |  | |
「相似の中心 定義」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
 | ||
「相似の中心 定義」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
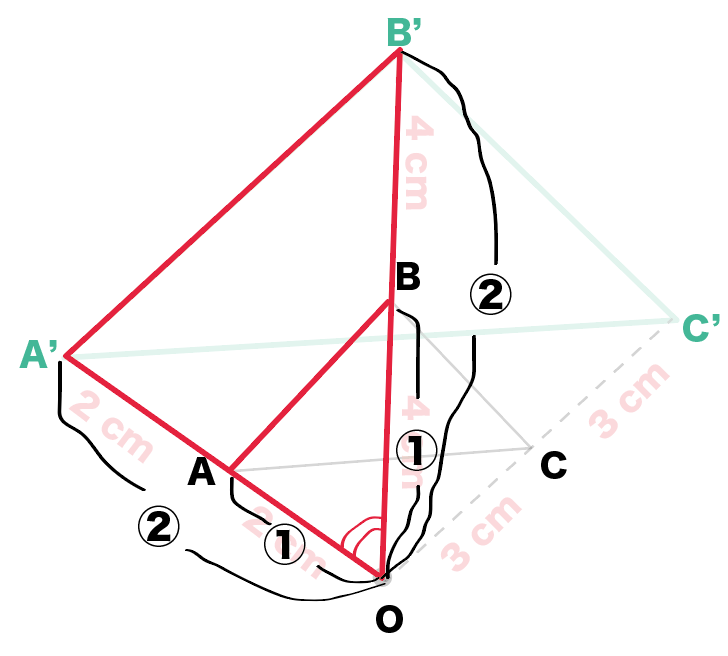 |  |  |
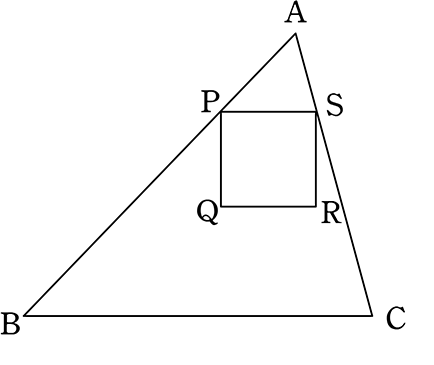
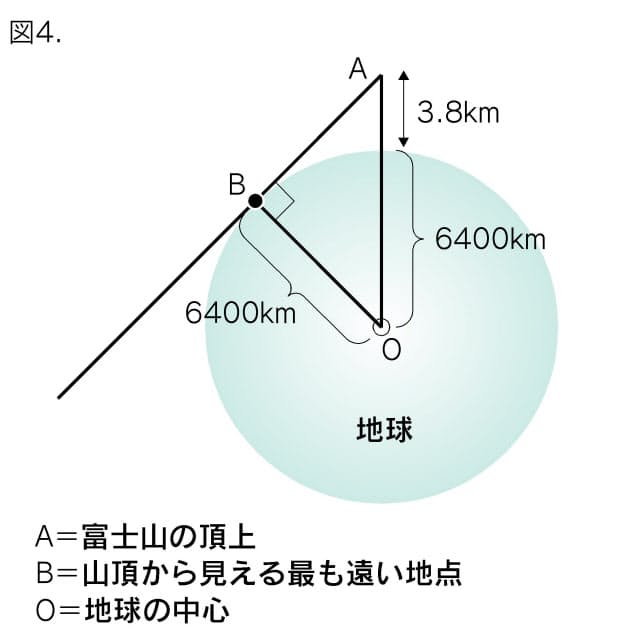
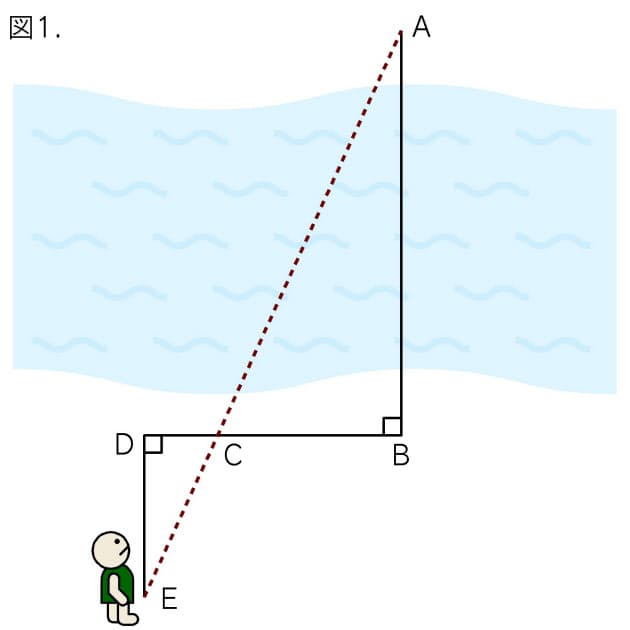
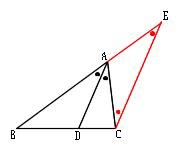
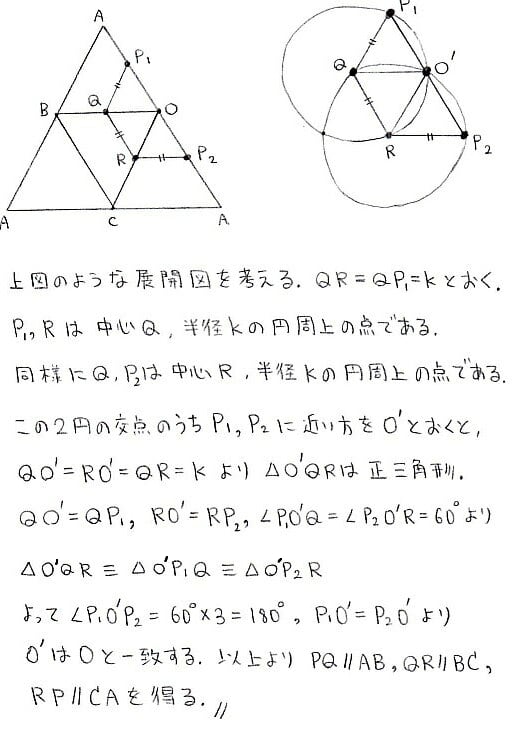
自己相似性条件によって定義された多くの集合は明示的に決定できる次元を持つ。大まかには、集合 e が自己相似であるとは、それが適当な集合値変換 ψ の不動点、すなわち ψ(e) = e となるときに言う。正確な定義は以下に与える 定理 r n 上の写像の列今回は中3で学習する 『相似な図形』の単元から 中点連結定理を利用した問題 について解説していきます。 特に、三角形を三等分するような問題がよく出題されているので それを取り上げて、基礎から解説していきます。 ちなみに 相似な図形の他
Incoming Term: 相似の中心 定義,




0 件のコメント:
コメントを投稿