Ken 次数の意味から5分でわかる!一次式と二次式の違い 一次式と二次式の違いがよくわからない!! 中学1年生の数学単元で 「一次式」と「二次式」 という言葉が登場します。 一次式とか二次式とか聞こえはかっこいい。一次不定方程式axby=cの整数解 3x5y=2 3x 5y = 2 のように,方程式の数よりも未知変数の数が多いような方程式のことです。 axby=c ax by = c という不定方程式の整数解について,重要な定理の証明と,実際に不定方程式の一般解を求める方法を説明します。 一次方程式(一次関数)の解(x)を求める 続いて一次方程式(一次関数)の解(x)を計算する方法を確認していきます。 解を求めるには、上と逆の操作をすればよく、y=2x5という一次関数では、 2x = y5 ⇔ x = (y5)/2という計算式をそのままエクセルで表現
1次関数 グラフ 直線の方程式
一次関数と方程式 解き方
一次関数と方程式 解き方-この基本式のうち、 a と b は定数(ていすう)と言い値が変わりません。 また x と y は変数(へんすう)と言い、 x の値が変われば y の値も変わっていくものです。 一次関数はグラフを使って表すことができます。例えば y =2 x 1 という一次関数は以下のようなグラフになります。この頁の目標 1次関数のグラフを見て,方程式が答えられるようにする. i 直線のグラフから「切片」と「傾き」を読み取れるようにする. ii 直線のグラフから1次関数の方程式を答えられるようにする. iii 傾きが分数になるときでも,直線のグラフから1次関数の方程式を答えられるよう



1
3 連立方程式とグラフ x,yについての連立方程式の解は,それぞれの方程式のグラフの交点の座標と一致する。 x k h y O y=k x=h 教科書 単元 14 一次関数と方程式 P77〜 啓林 _1_Keyワーク_数学_啓林_2年_Qindd 78 1714 中2数学:一次関数と方程式(2直線の交点の座標の求め方) 授業わかるーの byナオドット先生|中学数学のわかりやすい解説サイト ホーム 「一次関数」の章を一目で理解できるように、重要事項を最も簡単にまとめました。 1、一次関数とは何か (1)yがxの関数で、yがxの一次式で表わされるものを一次関数という 最初にいくらかの量があり、それから決まった割合で増えていく2つの量があるとき、2つの量の関係が一次関数
で表わされる微分方程式をn階線形微分方程式(nthorder linear differential equation)といいます.また を 係数関数(coefficient function), を入力関数(input function)といいます. のときこの方程式を同次方程式(homogeneous equation)といいます.この微分方程式の左辺を と省略した形で表わすことがよくあります平面の方程式 平面の方程式 一次方程式z = z0 a(x−x0)b(y −y0) が三次元空間内で表す図形はP0(x0,y0,z0) を通り、ベクトル ~n = a b −1 に垂直な平面である。( ~n は法線ベクトル) 、 とすると 上の方程式は次のように書き直せる:・エクセルで一次関数の解を計算する方法 ・エクセルで2つの座標を通る一次関数を求める方法 というテーマで解説していきます。 エクセルで一次方程式を計算し、グラフを書く方法 まず、一次関数とは、y = ax b という式で表されるものです。
一次関数のグラフ( 一次関数のグラフのまとめ~グラフの書き方) 一次関数のグラフ(式の求め方) 一次関数 と方程式 連立方程式 とグラフ 一次関数の利用1 一次関数の利用2(動点の問題) 二学期中間ご意見・ご感想・ご要望(バグ報告は こちら) バグに関する報告 (ご意見・ご感想・ご要望は こちら ) 計算バグ (入力値と間違ってる結果、正しい結果、参考資料など) 説明バグ (間違ってる説明文と正しい説明文など) アンケートは下記にお客様の声とし数学23章一次関数 「二元一次方程式と関数」<基本問題①> 組 番 氏名 次の問いに答えなさい。 (1)次のア~エの中で,二元一次方程式3χ-y=8の解になるのはどれですか。
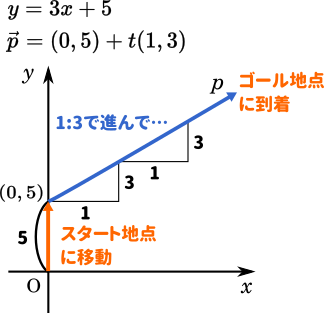



ベクトル方程式と媒介変数表示の仕組み やってることは一次関数と同じ Mm参考書




Excel エクセルで一次関数を計算し グラフを作る方法 一次関数の解を求める方法
これらを連立方程式で解いてやると \(a=1, b=7\)となるので 答えは、\(y=x7\)となります。 参考:一次関数式の作り方をパターン別に問題解説! 変域から式を求めるような問題では 切り取られたグラフをイメージして、座標を読み取りましょう。 単元 1次関数と方程式, 「一次関数と方程式です! 次の数学のノートまで時間がかなり開くかもです!(誰も待ってないとは思うけど、)」, 学年 中学2年生, キーワード ユキノート,一次関数,方程式,一次関数と方程式,中学,中2,数学,ユキ,math次の形の常微分方程式を1階線形常微分方程式といいます. y'P(x)y=Q(x) (1) 方程式(1)の右辺: Q(x) を 0 とおいてできる同次方程式 (この同次方程式は,変数分離形になり比較的容易に解けます) y'P(x)y=0 (2) の1つの解を u(x) とすると,方程式(1)の一般解は
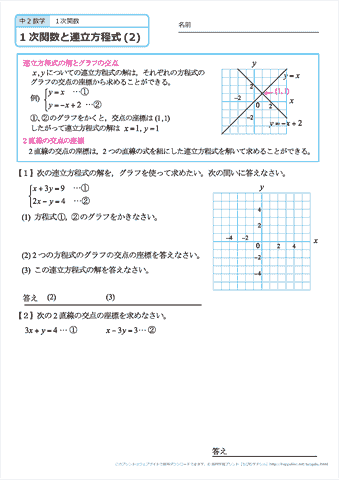



中学2年生 数学 1次関数と連立方程式 文章題 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




Mathematics 1次関数 6 応用問題の解き方 1 1次関数と図形 働きアリ
(2) 下の表は,ある一次関数について,x の値とy の値の関係を示したものです。 y をx の式で表しなさい。 x ・・・ -2 -1 0 1 2 ・・・ y ・・・ -1 2 5 8 11 ・・・ 6 二元一次方程式2x +y =6の解を座標とする点の全体を表すグラフを,下のアからエの/1/7 2年一次関数総合問題Lv3 5 (2) 点Pはlとx軸の交点 (誤)→点Bはlとx軸の交点 (正) 3年方程式文章題 (割合2)3 (1)解答 2番目の式 yの係数 97 100 (誤)→ 93 100 (正) 7 3年2乗に比例する関数総合問題4 5問題 点A, P, Qを頂点とする (誤)→点D, P, Qを頂点とする二元一次方程式を2つの変数 , の間の関数関係を表す式としてとらえ直すことで, その意味の理解を深めることができると考えられる。 指導に当たっては,二元一次方程式 =5を満たす と の値の組を



一次関数と一次方程式の違いと 二次関数と二次方程式の違いってなんです Yahoo 知恵袋
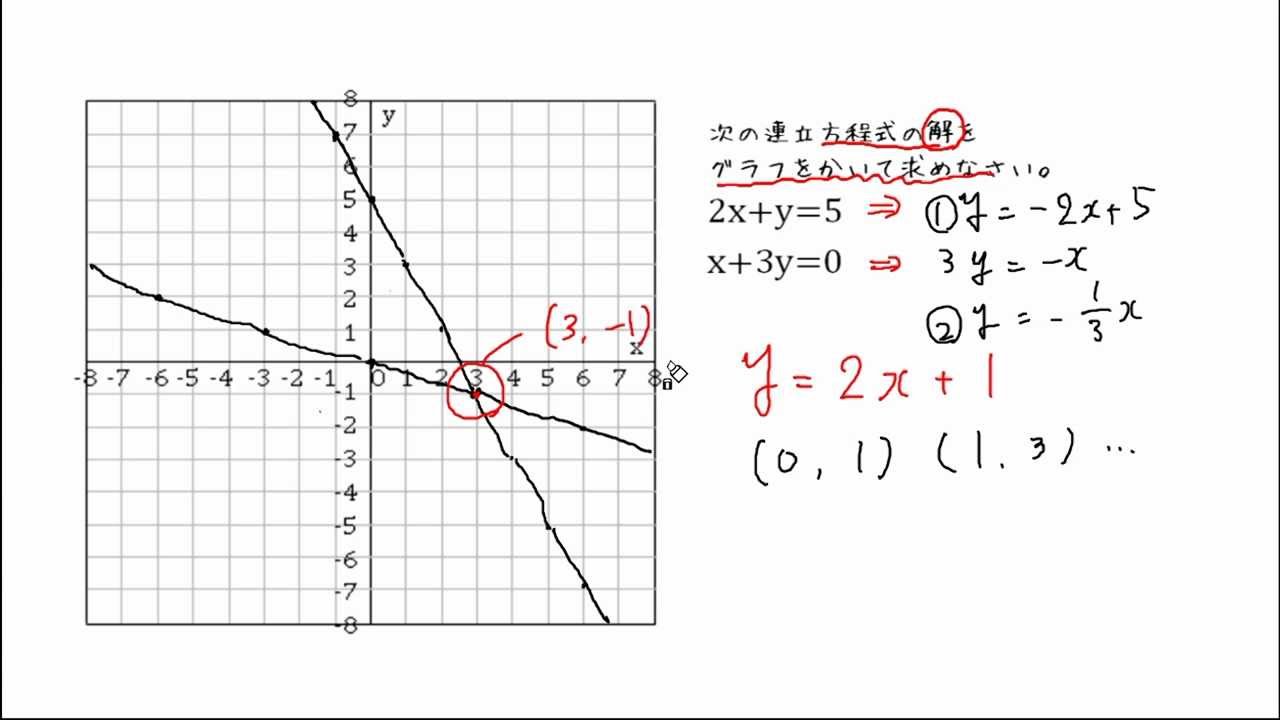



一次関数と連立方程式 Youtube
なお、この一次関数(直線の方程式)を式変形して以下のような形にします。 y = mx + k この方程式中のkがy切片(y軸と交わるところ)であることも併せて理解しておくといいです。 2点を通る直線の傾き、切片、方程式を計算してみよう問題代数方程式はさらに、一次方程式、二次方程式といったように、多項式の次数 (degree) d により d 次方程式 (dic equation, d th degree equation) に分類される。 四次以下の一変数代数方程式は多項式の係数に関する四則演算と根号を用いて解を表すことができる。技 2点の座標が与えられたときの一次関数の式を求め ることができる。 知 一次関数の変化の割合,傾き,切片の意味を式,グ ラフとの関連で理解している鏑 <二元一次方程式のグラフ>2-(1) 二元一次方程式のグラフはどうかけばいいのか,連




一次関数 二元一次方程式をグラフにする2つの書き方 Qikeru 学びを楽しくわかりやすく
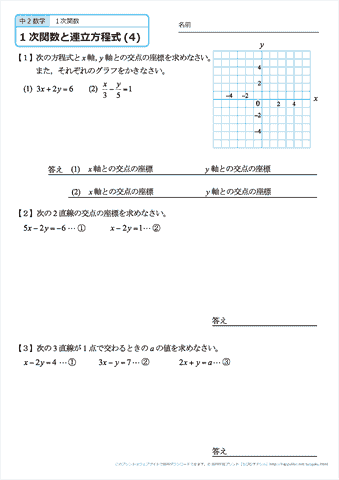



中学2年生 数学 1次関数と連立方程式 文章題 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
今回は中2で学習する 『一次関数』の単元から 直線の式の求め方について解説していくよ! ここでは、いろんなパターンの問題が出題されるので パターン別に例題を使って解説していきます。 傾き、切片が与えられる (1)傾きが5で、切片が-2であるわかったこと③一次関数と連立方程式のつながりを感じ たこところ④自由感想」とする。抽出する生徒は,学力 の上位群,中 位群,低 位群の中からそれぞれ1名ずつと する。量的側面については,連立方程式と一次関数との つながりに関するアンケートを分析 一次関数のグラフ( 式の求め方) パワーポイント教材(246k) 指導の流れは最初のスライドにあります。 ワークシートパック 一次関数と方程式 パワーポイント教材(244k) 指導の流れは最初のスライドにあります。



Http Www Juen Ac Jp G Katei Nunokawa Function 2 2 5 Pdf




一次関数 式の求め方をパターン別に問題解説 数スタ
傾き・切片標準形 一次関数の表す直線の式 y = ax b は、傾きと y切片を与えることによって一意的に決定される「傾き・切片(標準)形」(slopeintercept form) であり、座標平面上で直線を表す式としては他に「点・傾き(標準)形」(pointslope form) である = (点 (x 0, y 0) を通る、ただ一つの傾 一次関数の式「y = ax b」に切片と座標を代入してやればいいんだ。第6節 1次関数と方程式 ☆ 1次関数は式を用いて表されました。同じように式を用いるものとして方程式を学習し ました。ここでは関数と方程式の関わりについて調べていきましょう。 (1)2元1次方程式 2元1次方程式 2xy=7 で、xが次の値のときにyの値を求め
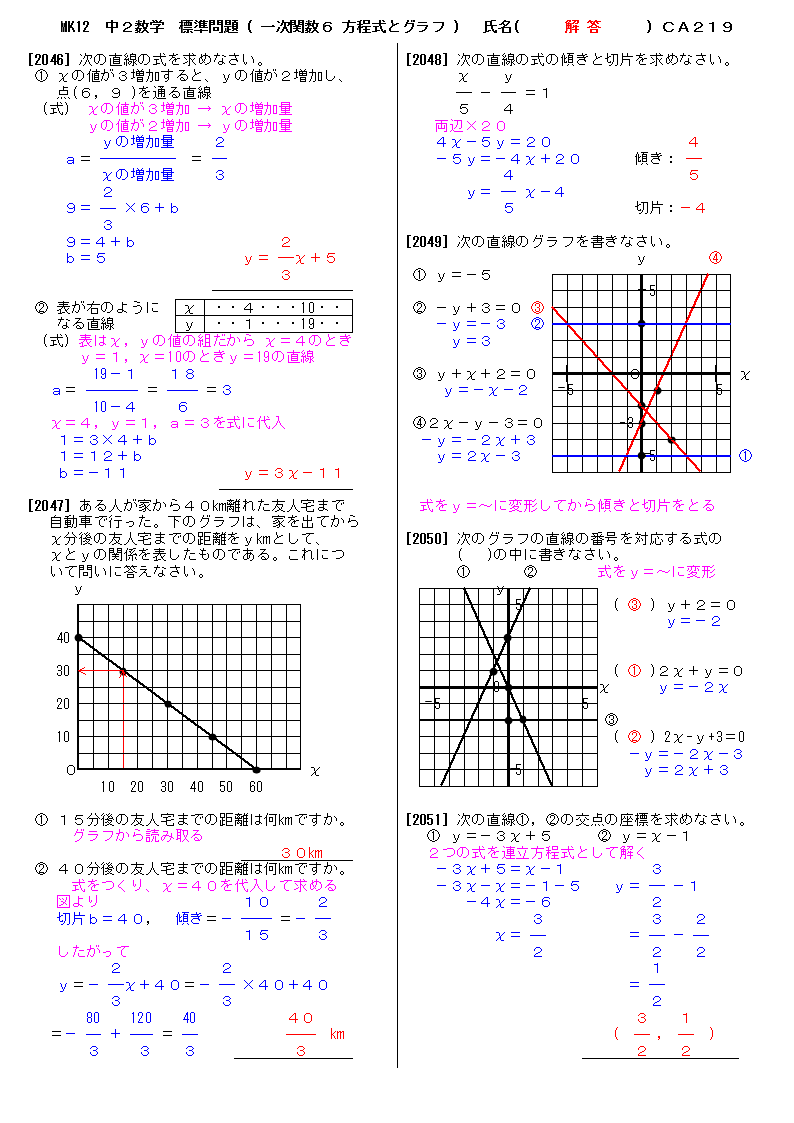



無料 中2数学 標準問題 解答プリント 219 一次関数6 方程式とグラフ




切片とは 超簡単 切片を一瞬で求める方法 傾きとの違い 高校生向け受験応援メディア 受験のミカタ
主な違い: 数学では、式は2つの式の間の等価性を表すために使用されます。 一方、関数は方程式よりもはるかに複雑です。 関数は、一組の入力と一組の対応する出力との間の関係を示すために使用される。 方程式と関数は、数学の主題である代数の2つの基本的な基礎です。一次方程式rxsyt z=uにおけるx,y,zの係数を並べた 実 3 次元数ベクトル ( r , s , t ) のことを言う。 ・平面 S の法線ベクトルは、・二元一次方程式を関数関係を表す式とみることで,二元一次方程式の解と一次関数のグラフの関係を見い出すことができる。 ・二元一次方程式のグラフをかくことができる。 13 連立方程式とグラフ




一次関数 式の求め方をパターン別に問題解説 数スタ



中2 1次関数4
2.二元一次方程式と一次関数の関係 上記のような生徒の実態は、二元一次方程式の解に対する代数的表現と 関数的表現の比較から特定された。そのため、二元一次方程式と一次関数 の概念間の関係について分析する必要があるだろう。 一次でも、二次でも、関数 f (x) に対して 等式 f (x)=0 が (一元)方程式です。 文字を増やして y=f (x) とすると、
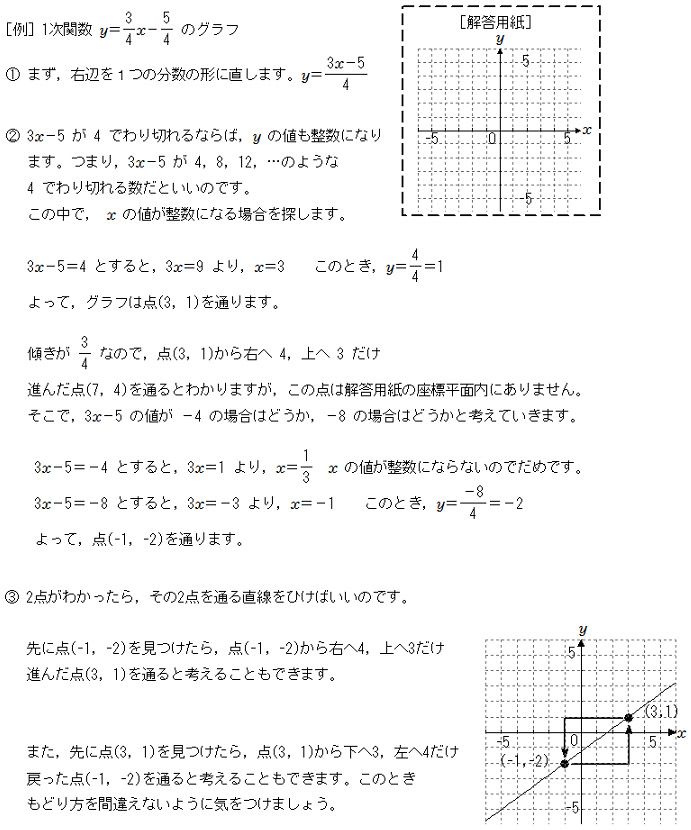



傾きや切片が分数であるグラフのかき方 中学英語 定期テスト対策 ベネッセ教育情報サイト
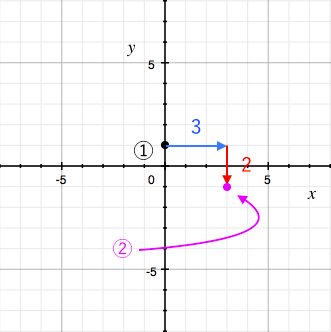



一次関数 グラフの書き方 苦手な数学を簡単に
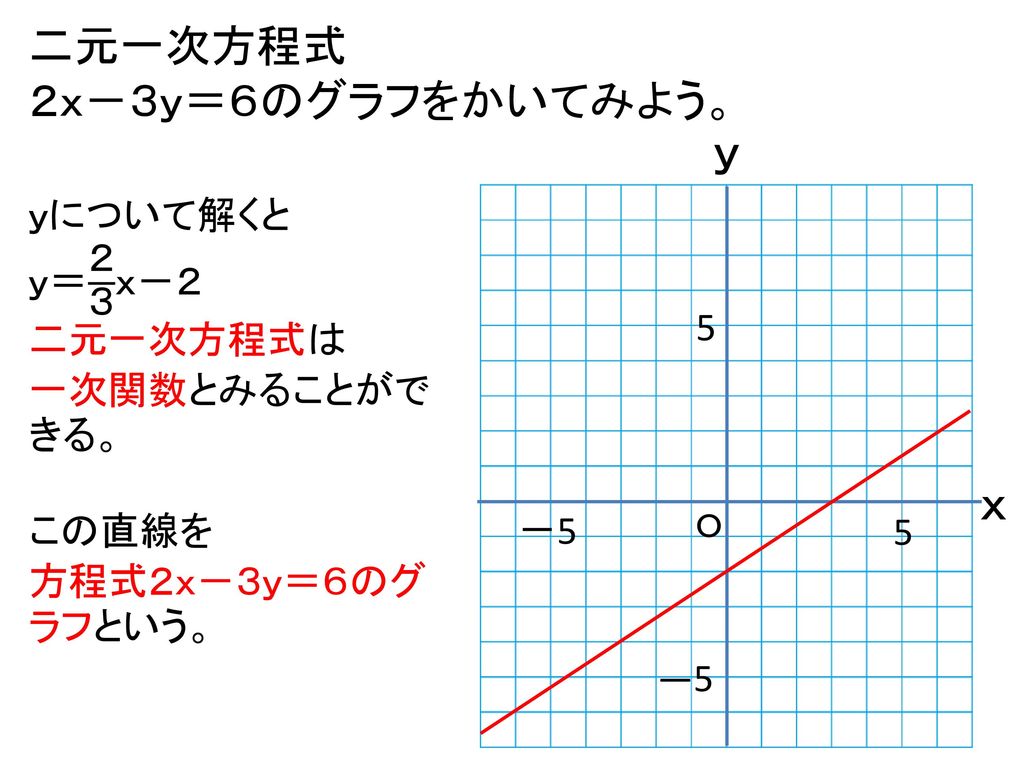



一次関数と方程式 本時の流れ ねらい 二元一次方程式をグラフに表すことができる 課題の提示 Yについて解き グラフをかく Ppt Download




一次関数のグラフがスラスラ書ける 見やすい図で徹底解説 高校生向け受験応援メディア 受験のミカタ




1次関数3 1次関数のグラフの交点と連立方程式の解 身勝手な主張



連立方程式とグラフ 中学2年 数学クラブ



一次関数とは グラフの書き方や一次関数の利用問題の解き方 受験辞典



1次関数 グラフ 直線の方程式



1



1次関数 グラフ 直線の方程式
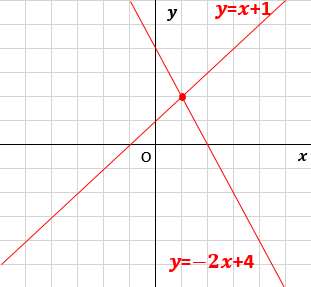



中2数学 一次関数と方程式 グラフの交点から連立方程式の解を求める 授業わかるーの Byナオドット先生 中学数学のわかりやすい解説サイト




数学 中2 32 一次関数の式をもとめる 基本編 Youtube




一次関数と方程式 本時の流れ ねらい 二元一次方程式をグラフに表すことができる 課題の提示 Yについて解き グラフをかく Ppt Download




一次関数のグラフの利用1 無料で使える中学学習プリント




中2 方程式と一次関数の利用 中2の方程式と一次関数の問題ですが 添付 Okwave
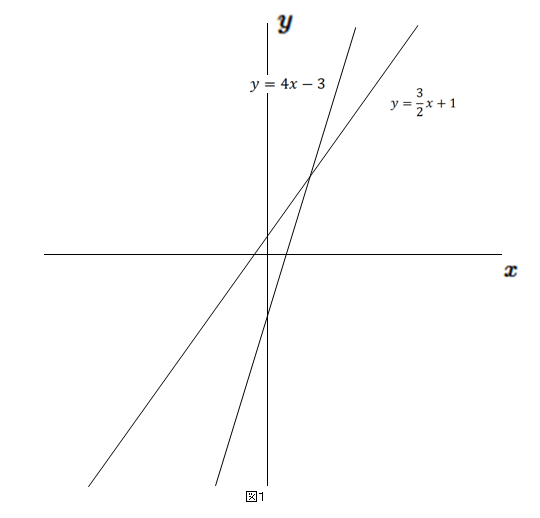



一次関数と連立方程式 2 ネット塾
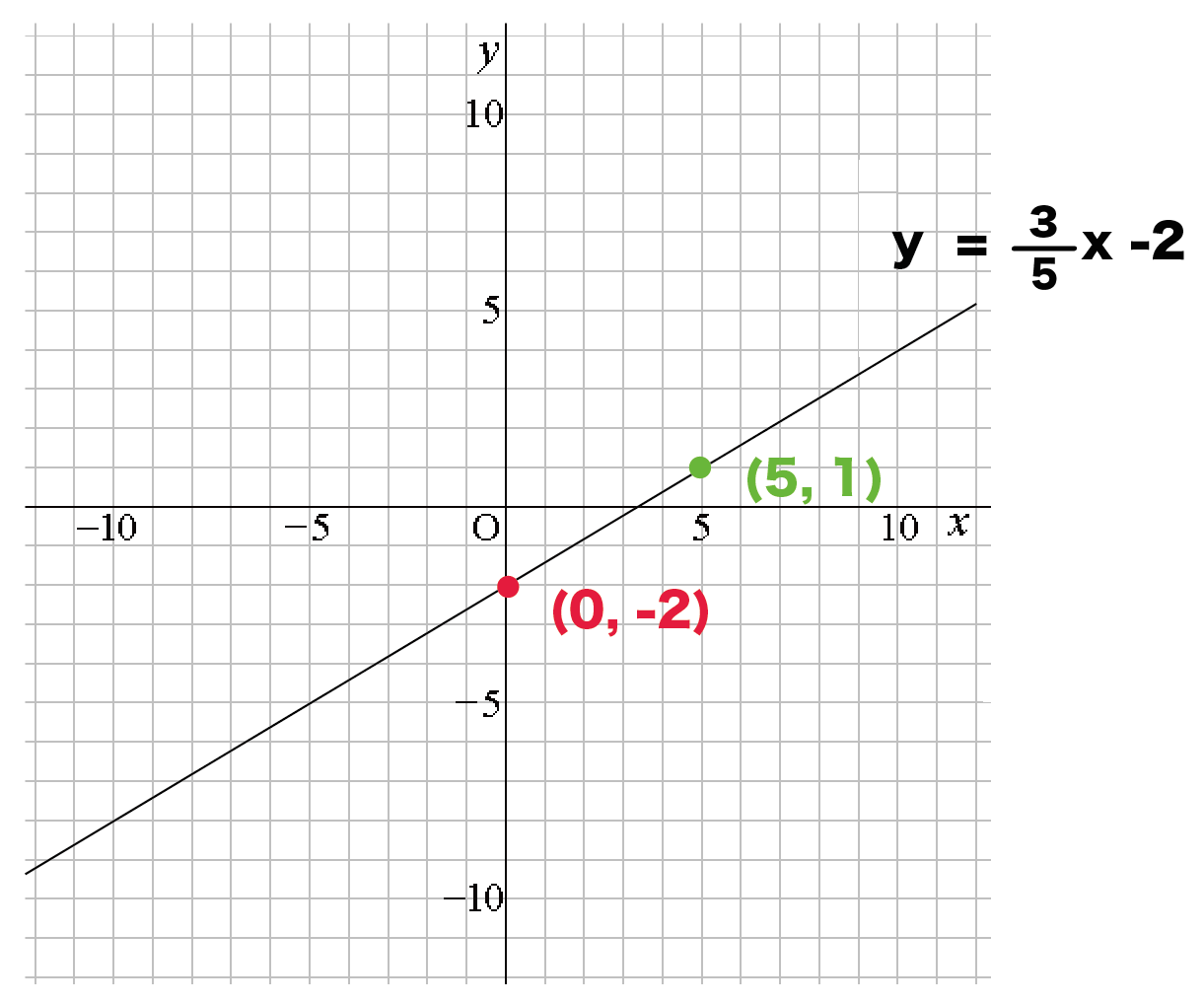



中2数学 一次関数のグラフの書き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
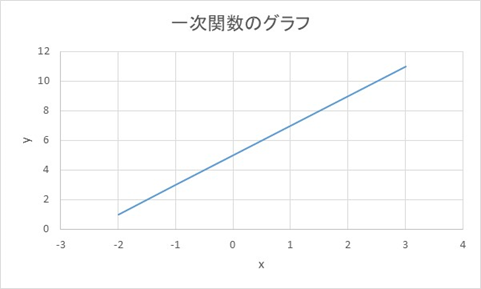



Excel エクセルにて1次関数 一次方程式 の計算 解や傾き とグラフ化の方法 複数も More E Life




数学 中2 36 一次関数の交点をだす 基本編 Youtube
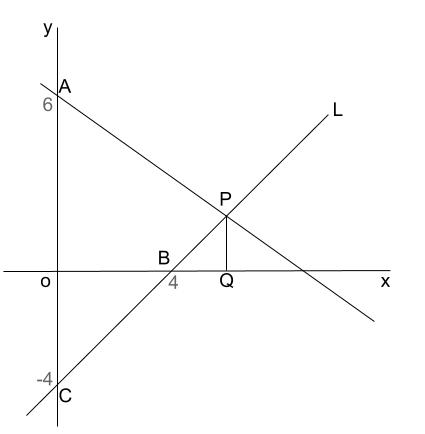



1次関数と方程式 中学数学の無料オンライン学習サイトchu Su
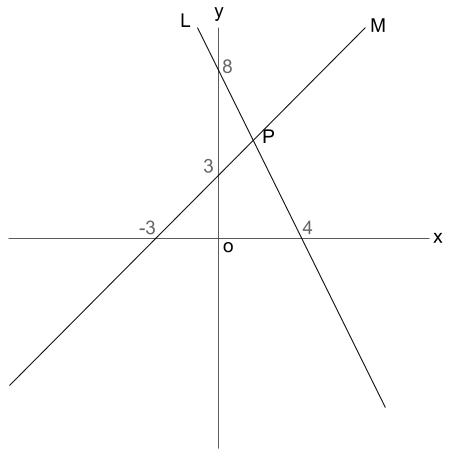



中学数学 2直線の交点 連立方程式とグラフ 中学数学の無料オンライン学習サイトchu Su
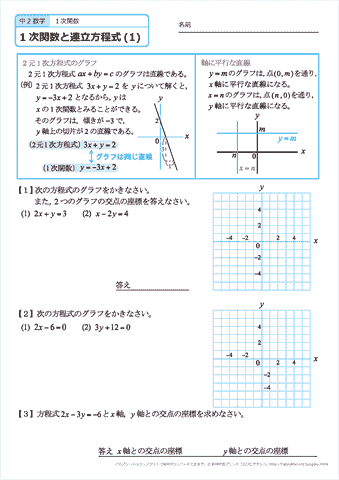



中学2年生 数学 1次関数と連立方程式 文章題 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中2数学 1次関数 3 2 連立方程式とグラフ Youtube




一次関数の式を決定1 無料で使える中学学習プリント
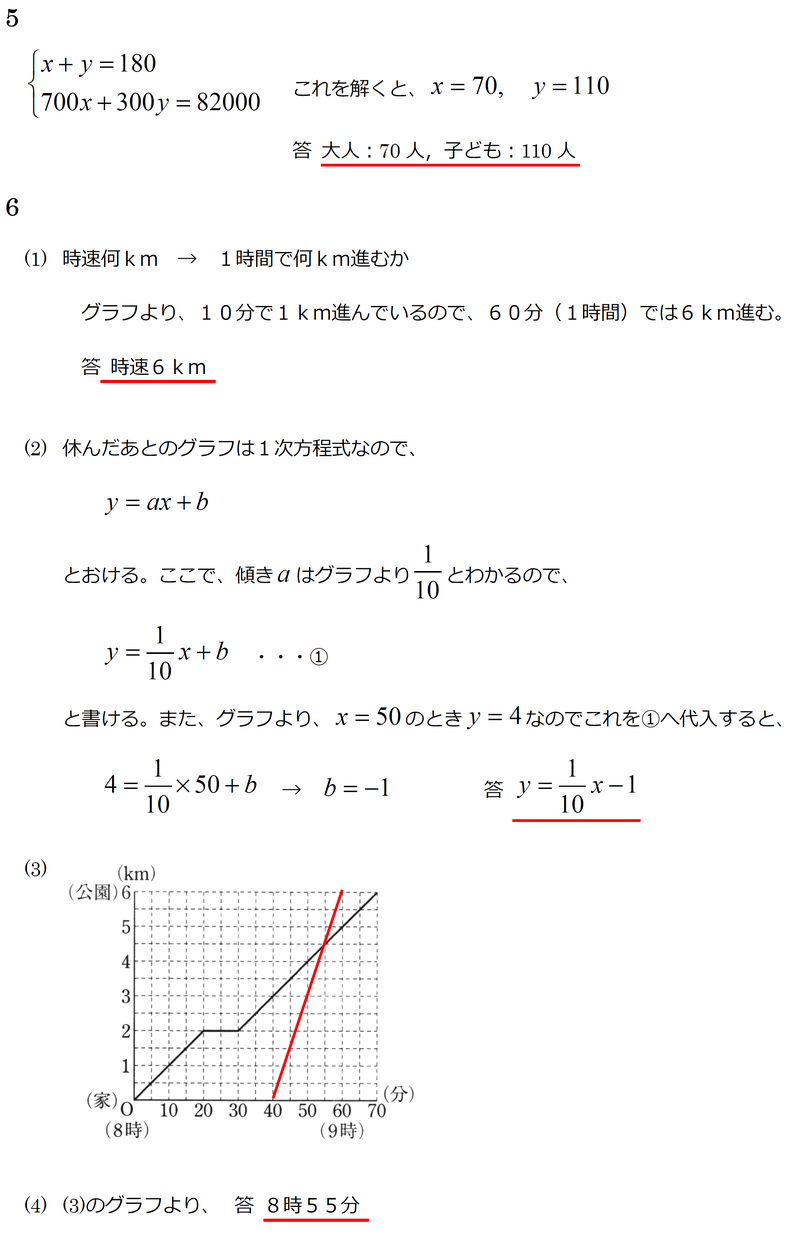



中学 数学 実力テスト 過去問 連立方程式 1次関数の利用 問題と解答 赤城 ᐡᐤᐡ
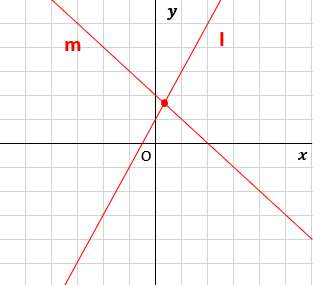



中2数学 一次関数と方程式 2直線の交点の座標の求め方 授業わかるーの Byナオドット先生 中学数学のわかりやすい解説サイト



1




切片が分数の時どうやってグラフを書くのかがわかりません 教えて欲しいです Clear
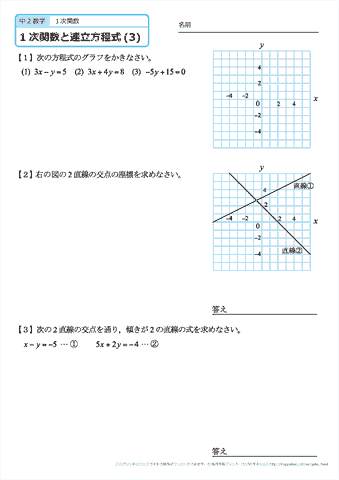



中学2年生 数学 1次関数と連立方程式 文章題 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
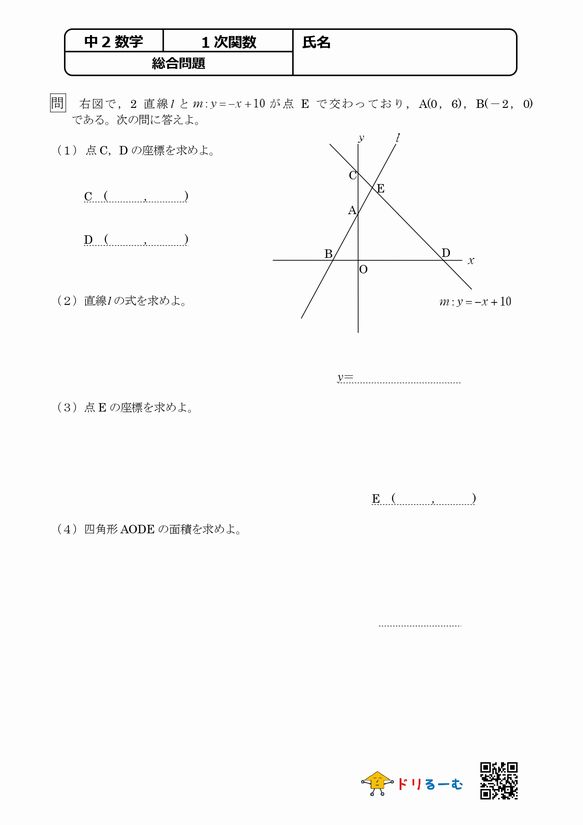



一次関数 総合問題 ドリるーむ




一次関数 連立方程式とグラフの関係 苦手な数学を簡単に




中学2年生 一次関数 連立方程式の解をグラフを使って求める問題です 4 5 のグ Clear




一次関数の利用 です Clear




0以上 一次 関数 の 解き方 シモネタ




方程式と関数の違いを理解しよう 理系のための備忘録



1



連立方程式とグラフ




一次関数 二元一次方程式をグラフにする2つの書き方 Qikeru 学びを楽しくわかりやすく
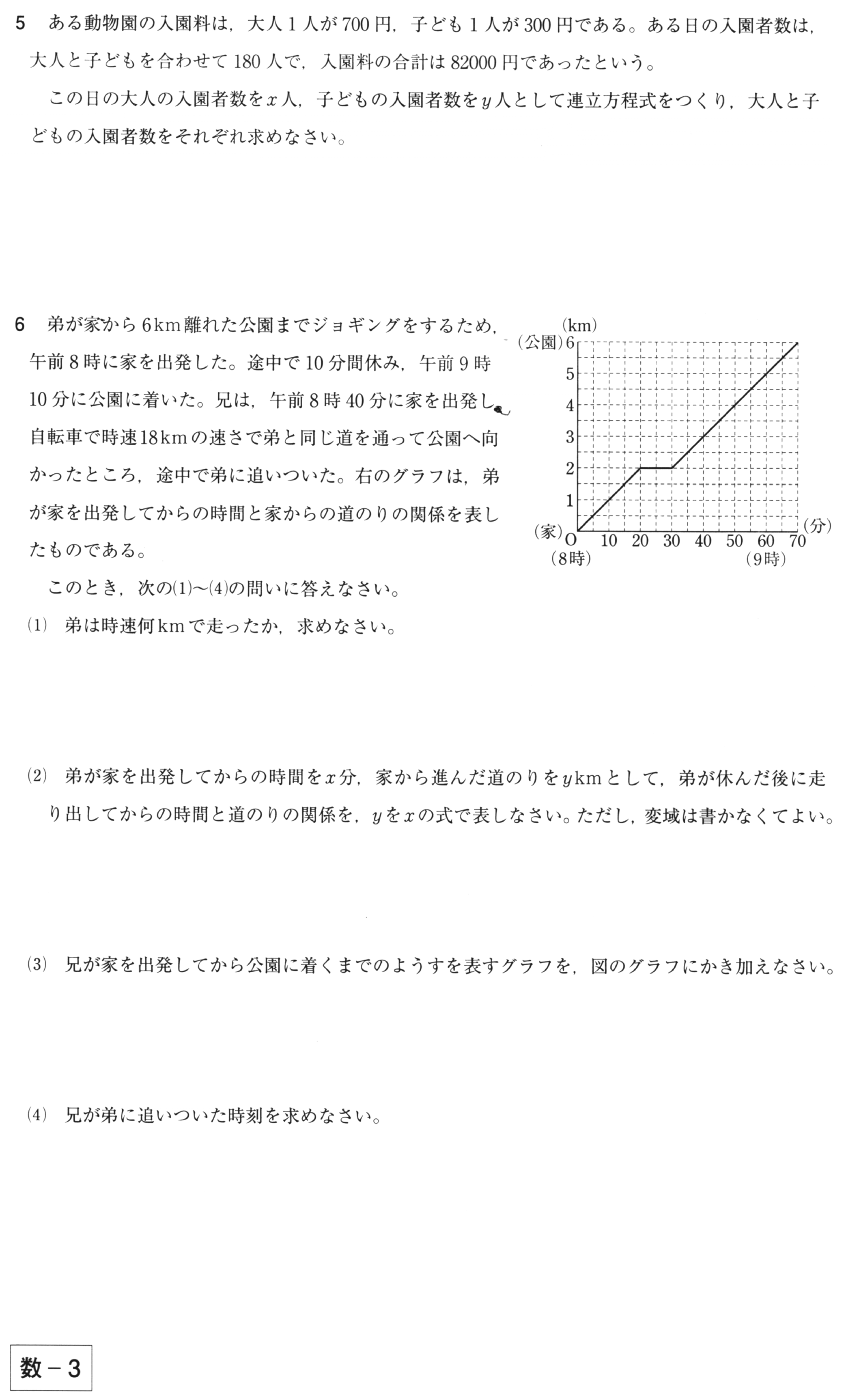



中学 数学 実力テスト 過去問 連立方程式 1次関数の利用 問題と解答 赤城 ᐡᐤᐡ




一次関数の問題の解き方 7パターン 数学fun



一次関数とは グラフの書き方や一次関数の利用問題の解き方 受験辞典
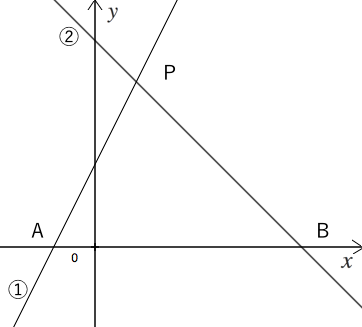



一次関数の利用 2直線が交わる 苦手な数学を簡単に
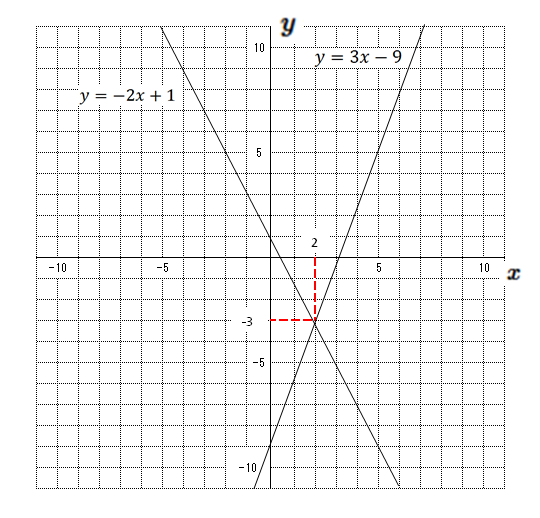



一次関数と連立方程式 1 ネット塾
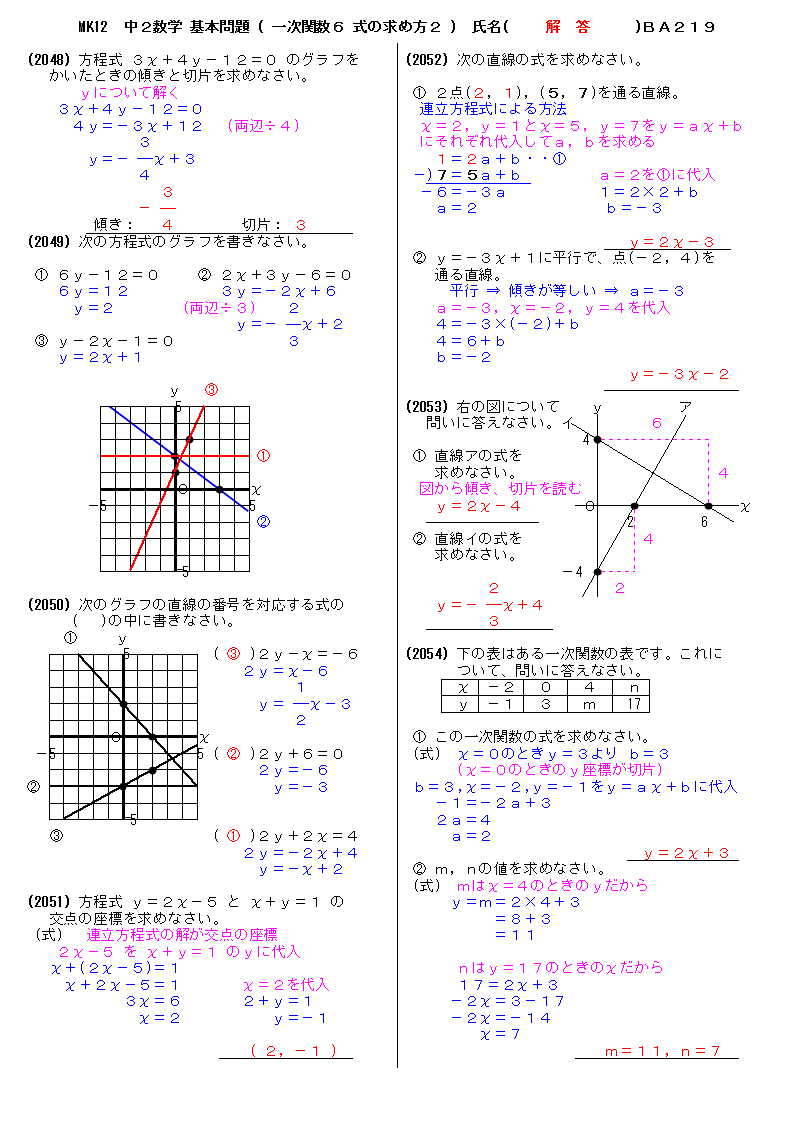



無料 中2数学 基本問題 解答プリント 219 一次関数6 式の求め方2
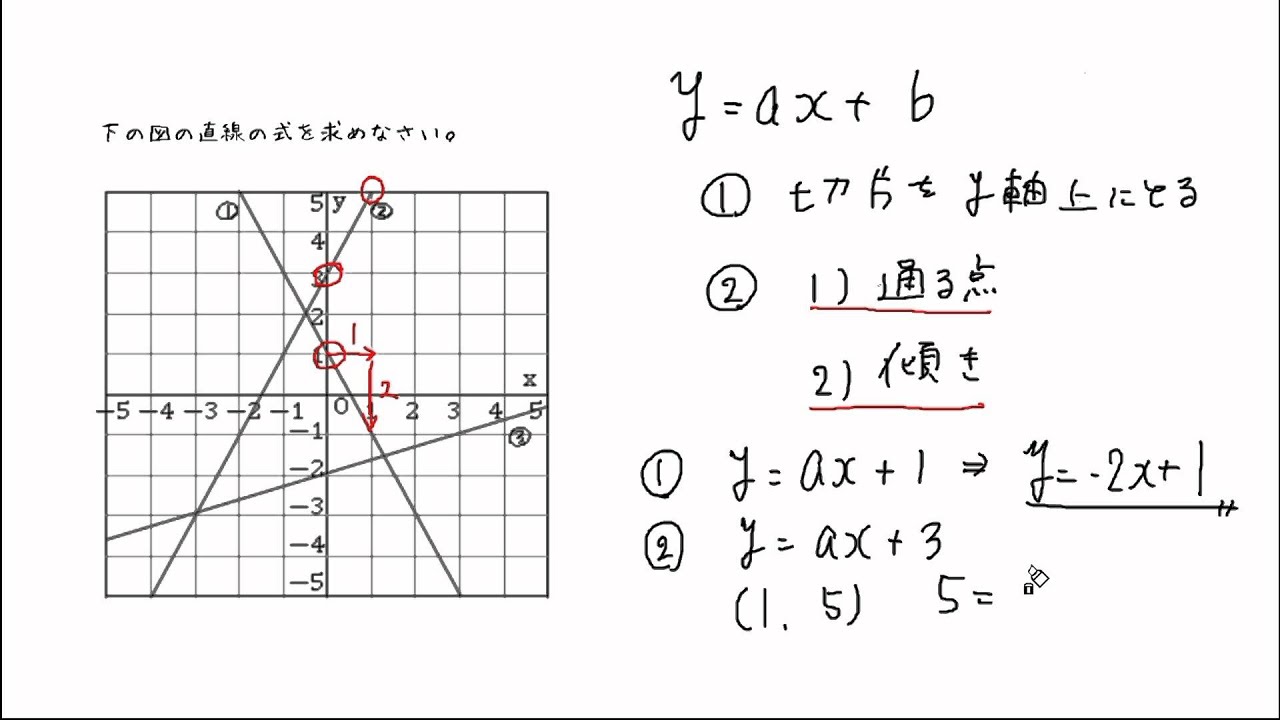



グラフから一次関数の式をもとめる Youtube




1次関数 2点を通る直線の式の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
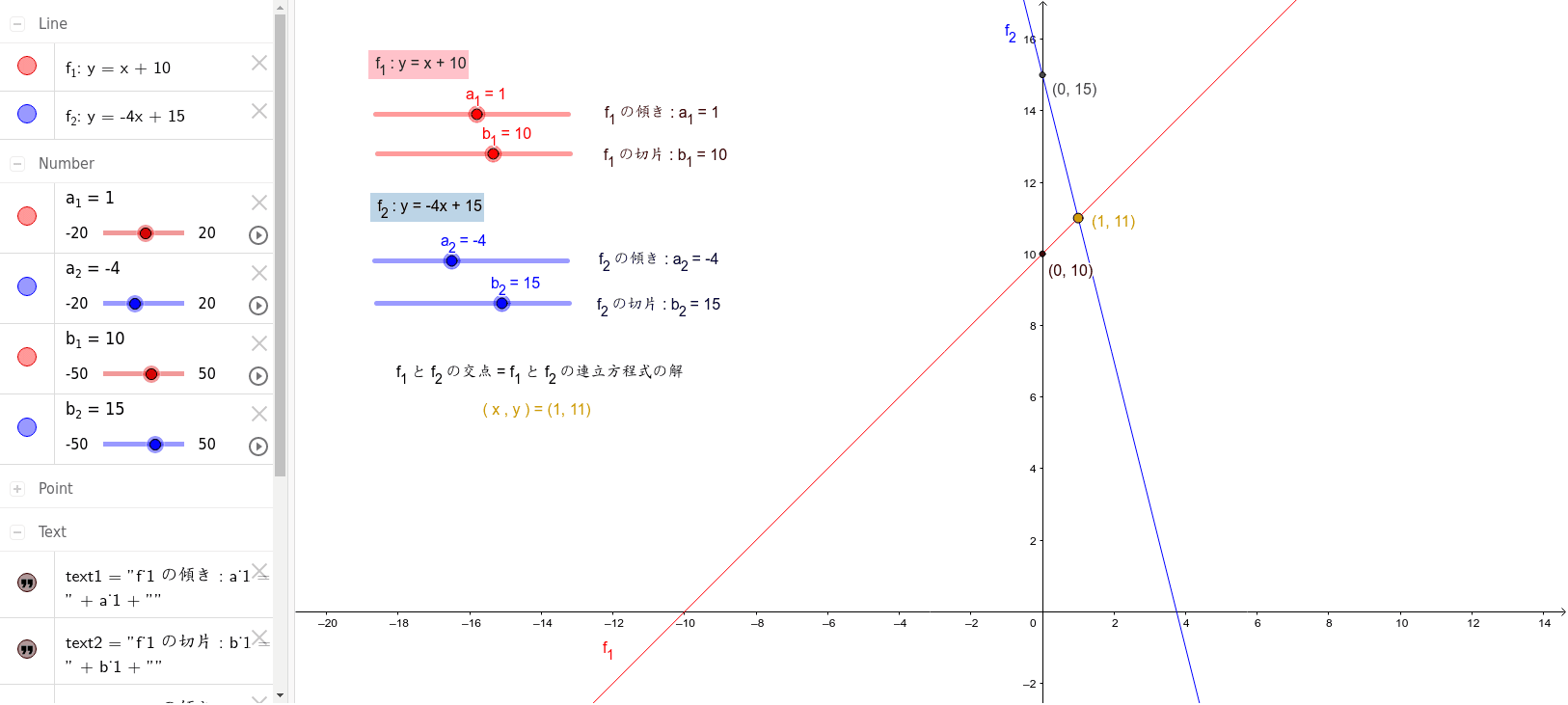



一次関数の交点と連立方程式の解 Geogebra
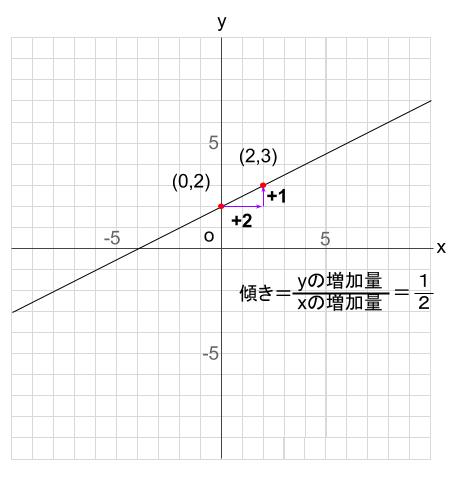



中学数学 1次関数 グラフの読み取り 中学数学の無料オンライン学習サイトchu Su
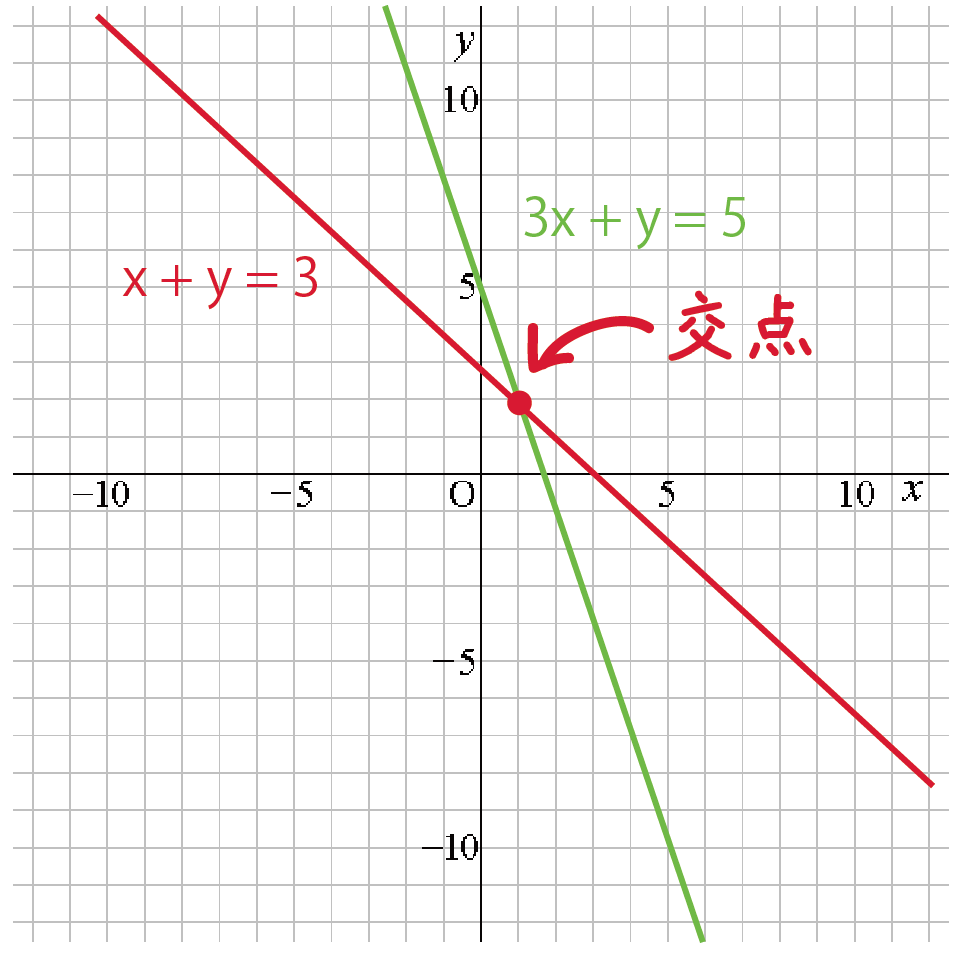



一次関数 グラフから連立方程式の解を求める3つのステップ Qikeru 学びを楽しくわかりやすく




中学2年生の数学 1次関数と正方形 長方形 塾講師が数学をやりmath




一次関数 表から式を求めるやり方についてイチから解説 Youtube




一次関数 グラフから連立方程式の解を求める3つのステップ Qikeru 学びを楽しくわかりやすく



超速まとめ 一次関数 一次関数の式 変化の割合 グラフ 二元一次方程式 Shun Ei Note




中学2年生 数学 1次関数と連立方程式 文章題 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
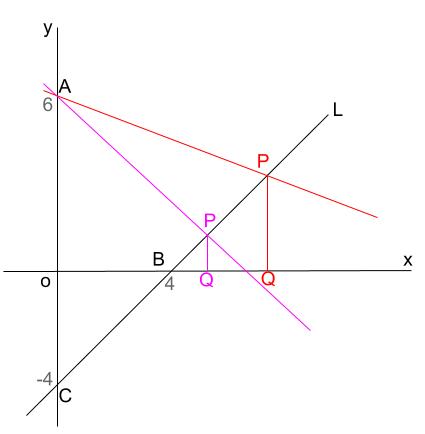



1次関数と方程式 中学数学の無料オンライン学習サイトchu Su
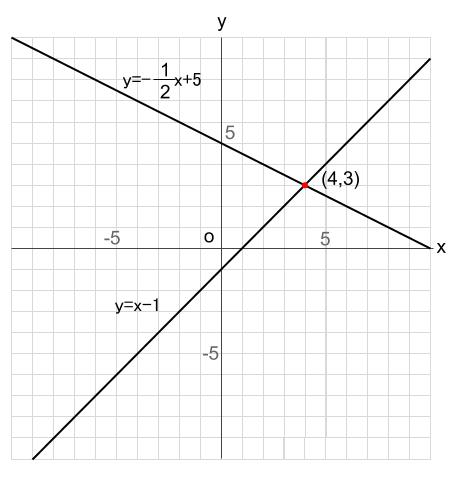



中学数学 2直線の交点 連立方程式とグラフ 中学数学の無料オンライン学習サイトchu Su
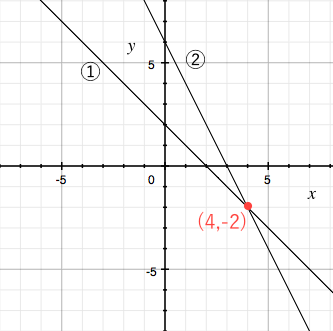



一次関数 連立方程式とグラフの関係 苦手な数学を簡単に
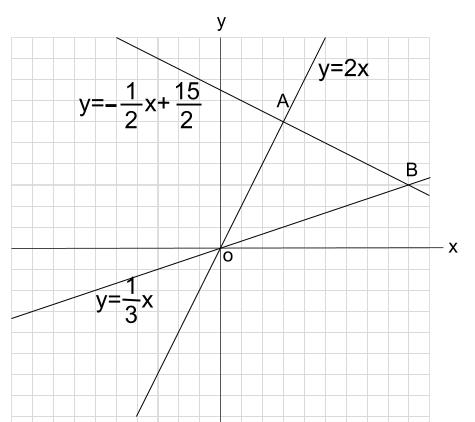



中学数学 1次関数と三角形の面積 その2 中学数学の無料オンライン学習サイトchu Su




次の条件を満たす一次関数の式を求めなさい Clear
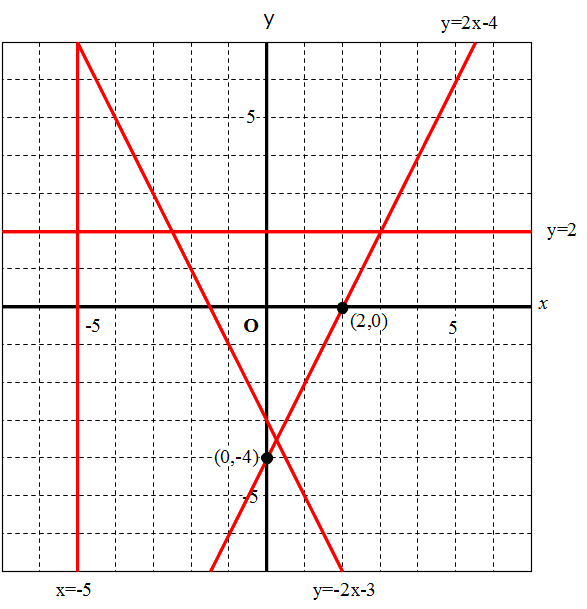



Math 超速まとめ 一次関数 一次関数の式 変化の割合 グラフ 二元一次方程式 働きアリ



一次関数 式の求め方をパターン別に問題解説 数スタ




一次関数と方程式 の問題 中学2年の数学 Okwave




一次関数 二元一次方程式をグラフにする2つの書き方 Qikeru 学びを楽しくわかりやすく
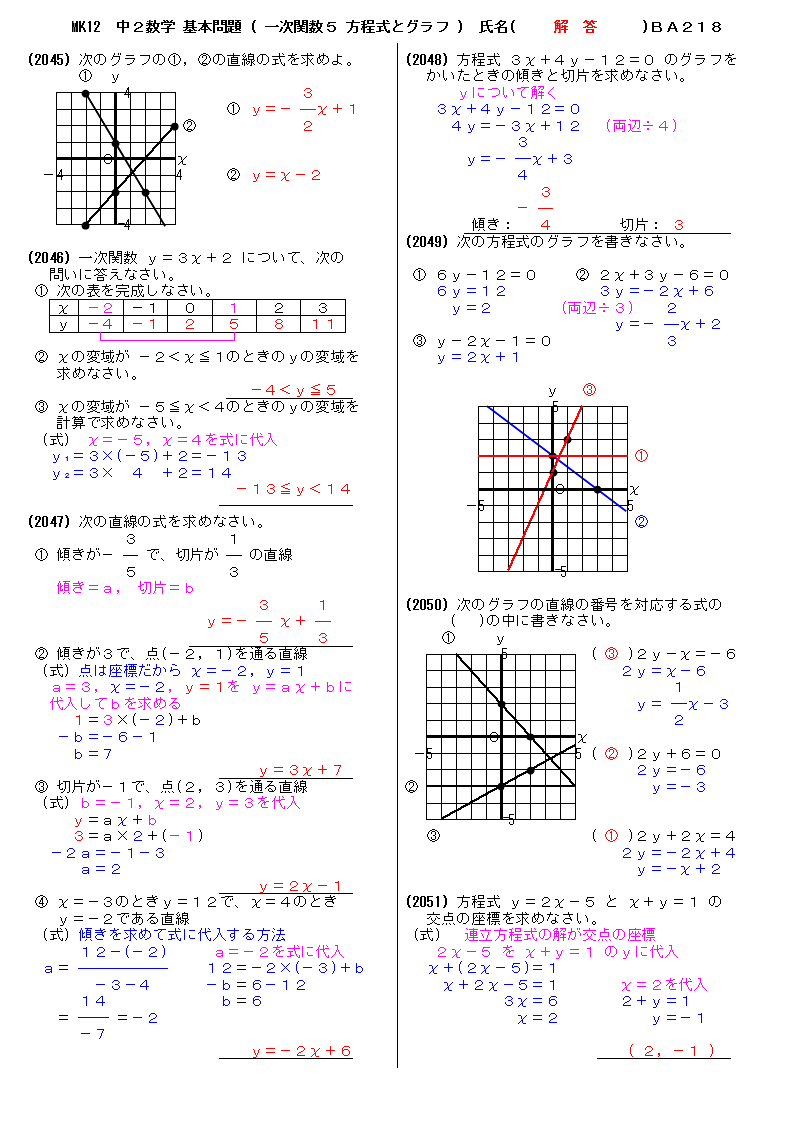



無料 中2数学 基本問題 解答プリント 218 一次関数5 方程式とグラフ



連立方程式と一次関数 名古屋市北区の学習塾は思考力を育む 泰成スクール




1次関数 1次関数の式の求め方 中学数学 定期テスト対策サイト




一次関数の傾きと切片を求める問題 Irohabook




一次関数のグラフがスラスラ書ける 見やすい図で徹底解説 高校生向け受験応援メディア 受験のミカタ
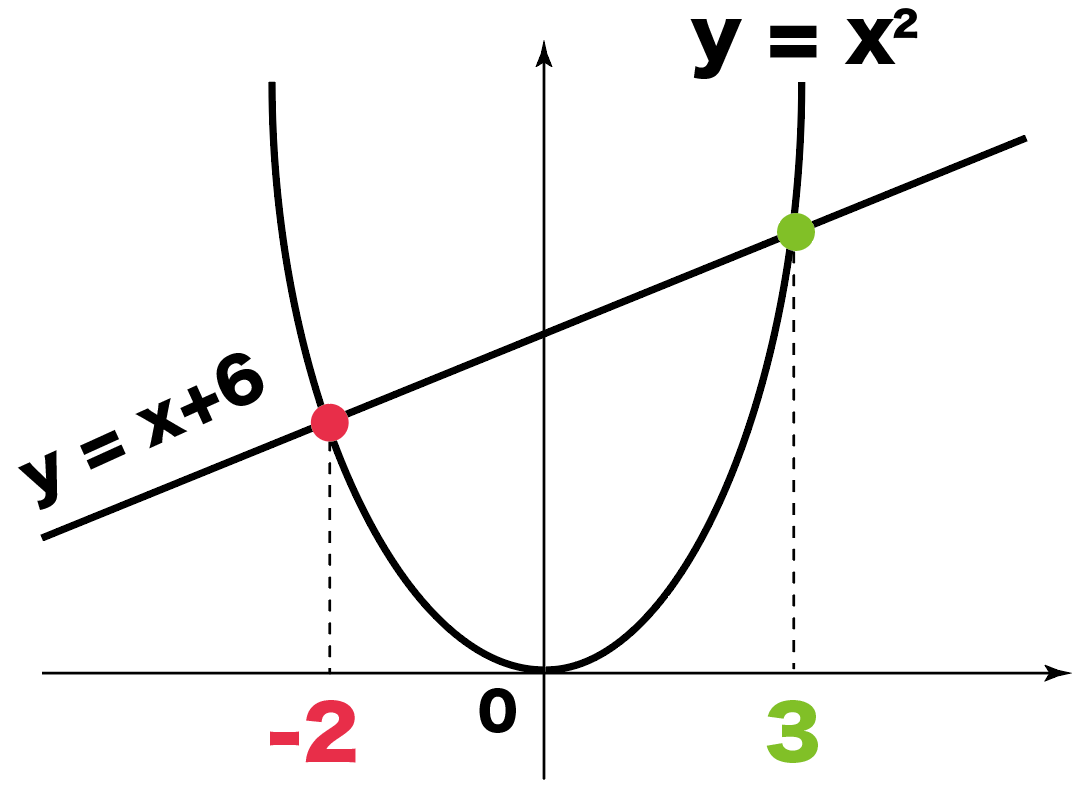



一次関数と二次関数の交点の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
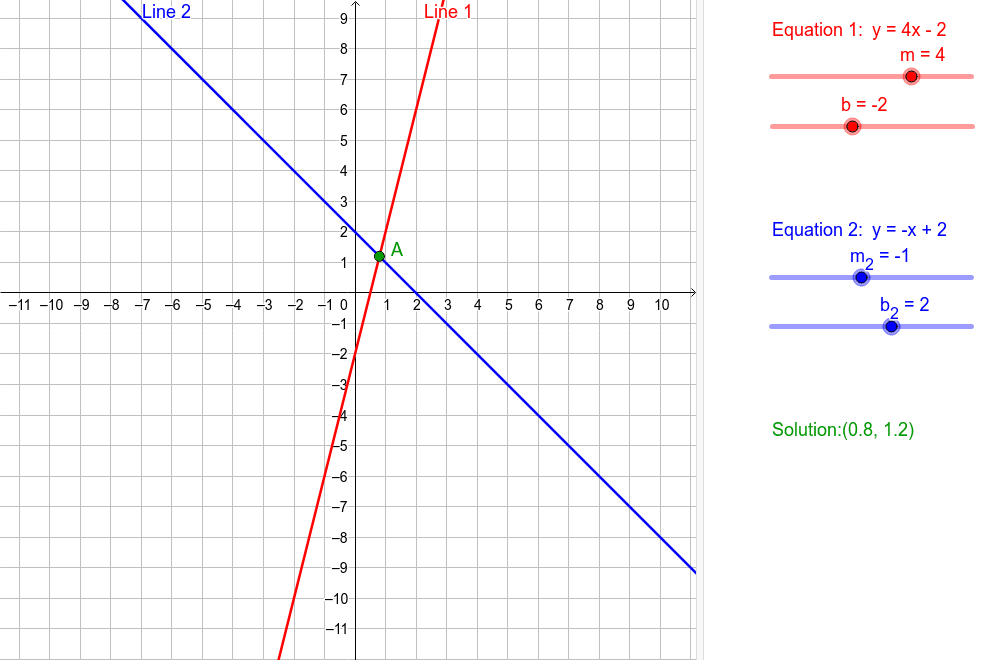



1次関数と方程式 Geogebra




数学 一次関数 中学生 数学のノート Clear
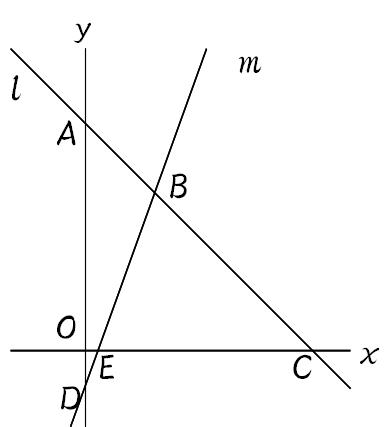



Mathematics 1次関数 6 応用問題の解き方 1 1次関数と図形 働きアリ
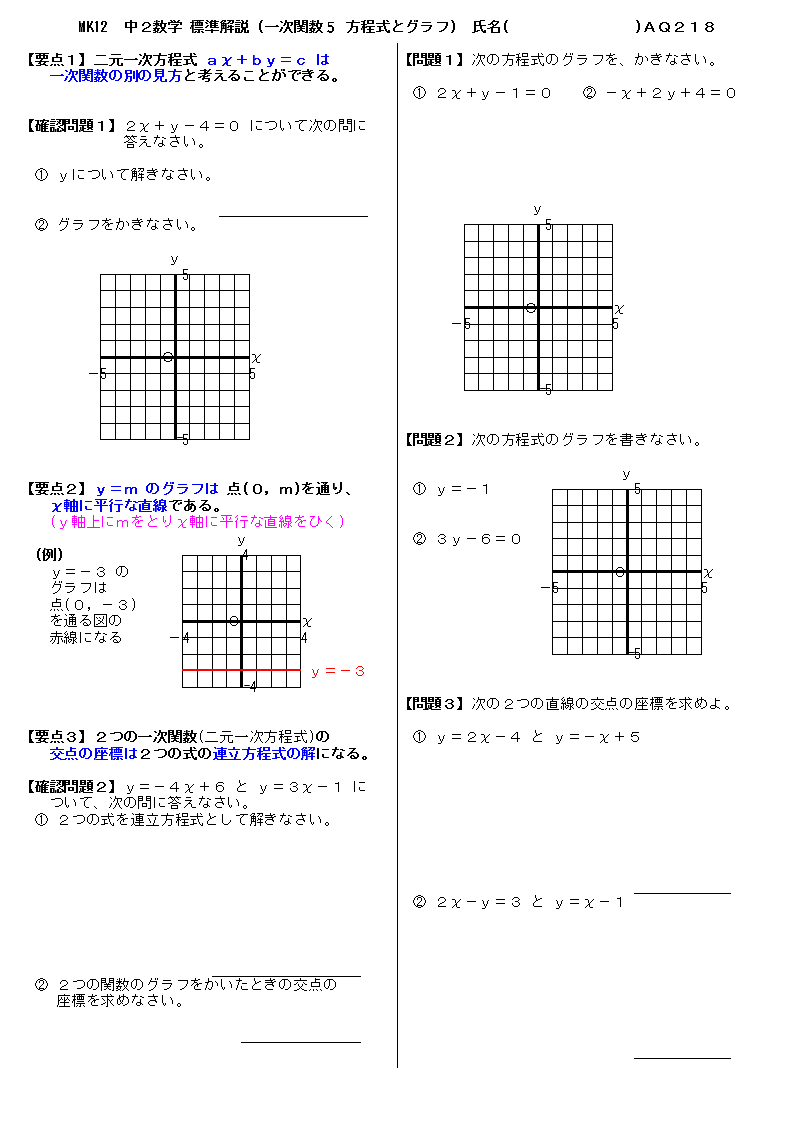



無料 中2数学 基本解説 問題プリント 218 一次関数6 方程式とグラフ
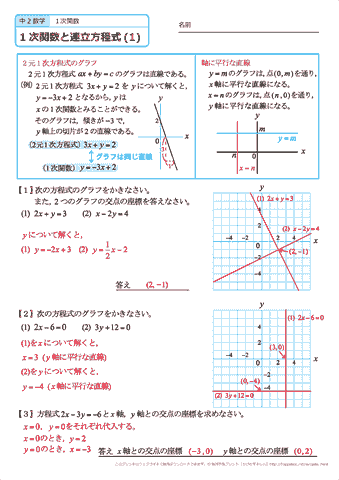



中学2年生 数学 1次関数と連立方程式 文章題 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




Excel エクセルで一次関数を計算し グラフを作る方法 一次関数の解を求める方法




課題学習の指導 数学




一次関数 二元一次方程式をグラフにする2つの書き方 Qikeru 学びを楽しくわかりやすく



中2 1次関数4
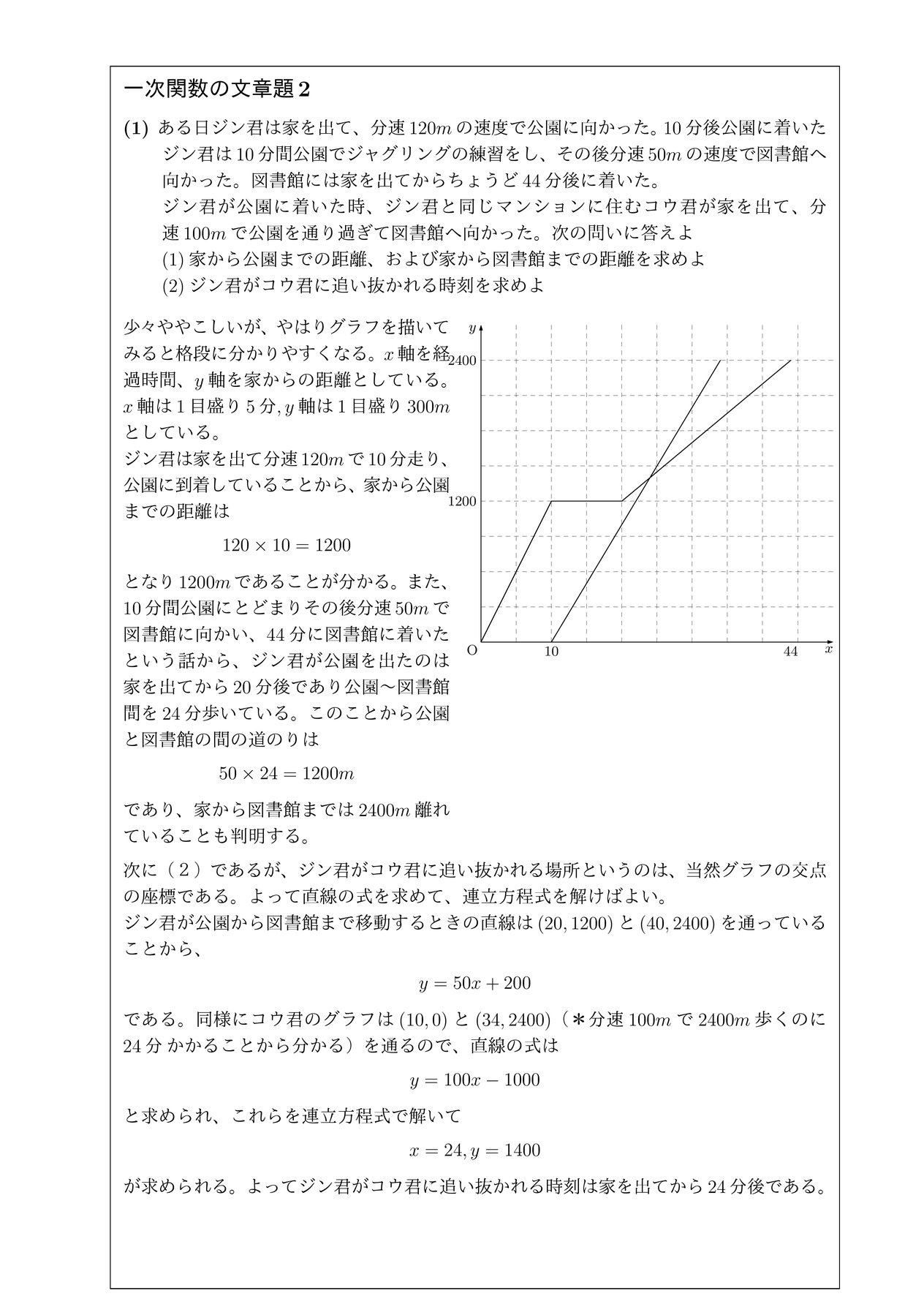



一次関数の文章題 道のりと時間 チーム エン




一次関数 式の求め方をパターン別に問題解説 数スタ




数学 一次関数 中学生 数学のノート Clear




1次関数と2元1次方程式の違い Youtube
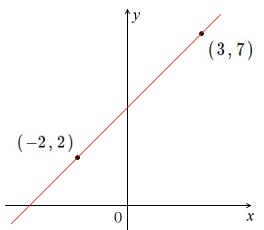



1次関数の交点の座標とグラフから直線の方程式を求める方法
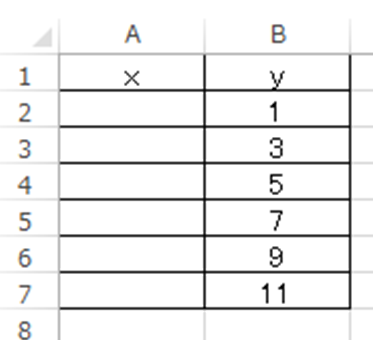



Excel エクセルにて1次関数 一次方程式 の計算 解や傾き とグラフ化の方法 複数も More E Life




切片が分からないときの一次関数の式の求め方 チーム エン
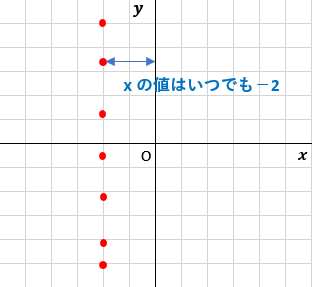



中2数学 一次関数と方程式 X Y グラフ Xが数字 Yが数字だけ の書き方 授業わかるーの Byナオドット先生 中学数学のわかりやすい解説サイト




1次方程式と1次関数 数学i フリー教材開発コミュニティ Ftext



1




2点から一次関数の式を求める チーム エン




こんな風に なぜ連立方程式で交点がわかるんですか Clear



0 件のコメント:
コメントを投稿