同次形微分方程式 さて,次の問題は どのようなときに \(\displaystyle \frac{y}{x} = u\) の置き換えが有効か? です。 \(\displaystyle \frac{y}{x} = u\) の置き換えにより変数分離形に変形できる微分方程式を 同次形微分方程式 とよびます。 どのようにしたら,ある微分方程式が同次形であることを見抜ける単元 三平方の定理 三角定規 15度 直角三角形 整数問題 証明問題 神奈川 平行四辺形 三平方の定理 円 直交する弦 相似 メネラウス 三平方の定理 神奈川 入試 平行線の錯角と同位角 循環小数・有理数・無限小数・41の倍数 中点連結定理 相似 内接円・外接円・三平方の定理 連立方程式 計算三角形の方程式について 船橋啓明高等学校新堀弘騏 平面上の直線や円の方程式は,かなり以前に見つかっており,よく,使われもして いる。しかしながら,三角形の方程式は長い間,見出そうと努力する者がいなかった。

利用双曲线的特征三角形解高考题 知乎
三角形方程式
三角形方程式-正三角形と方程式 \(x^31=0\)、正方形と方程式 \(x^41=0\) 複素平面(ガウス平面)に、実数の1を起点として、単位円上に正三角形と正四角形(正方形)を書きます。 「それがなんなん?」と思うかも数学Ⅱ ラジオ第2放送 毎週 水曜日・木曜日 午後7:50〜8:10 ※この番組は、21年度の新作です。




Watlow 三角形和y 型电路方程式
三角方程式 数学Ⅰで学習した三角方程式と大差はありません。 角の範囲が \(180°\) をこえただけです。 単位円による解法とグラフによる解法があります。 単位円による解法を断然おすすめします。 例 ベクトル方程式で三角形の外接円の中心の位置ベクトルを求める これは、ここをクリックした先の問題の解答です。 《解答の式の一覧》 以下の解答の式で覚えるべき最も重要な式は第14の解の式です。(第3の解,第7の解,第10の解とほぼ同じ式です) (最も重要な式を最初に書かな動機 有限要素法に関する記事の多くは、ポアソン方程式を取り上げています。 二次元を扱う場合、要素分割は大抵、三角形一次要素か四角形要素であることが多く、三角形二次要素にフォーカスされたものはそれほど多くないです。 そのため、この
高校数学Ⅱ 三角関数 検索用コード \sin\theta=k,\ \cos\theta=k,\ \tan\theta=k}}$の形の三角方程式・不等式を\textbf {基本型}と呼ぶことにする \\ 2zh 数Iの三角比分野で学習したとおり,\ 基本型は$\bm {\textcolor {red} {定義に基づいて図形的に解く}}$のであった 平行な直線の方程式 2つの直線 y = m1xn1 y = m 1 x n 1, y = m2x n2 y = m 2 x n 2 について、2直線が平行であることと m1 = m2 m 1 = m 2 であることは同値である。 x の係数のことが「傾き」を表していることを考えれば、「同じだけ傾いているのだから平行だ」という105 Graphical Solutions of Trigonometric Equations 三角方程式的图解法 (1) Sketch on the same diagram, the curves and for the interval State the number of
三角形の外接円の方程式}}}} \\\\ 5zh 三角形の外接円の方程式は,\ 結局は\textbf {\textcolor {blue} {座標平面上の異なる3点を通る円の方程式}}である 3点の座標から円の方程式を求める場合,\ 一般形を利用する}}のが基本である \\\\ $\textcolor {red} {x^2y^2lxmyn=0 図形と方程式|三角形の重心の座標について 今回は、三角形の重心の座標について学習しましょう。 三角形の重心は、中点や内分点などと共に頻出です。 また、後で学習するベクトルでも頻繁に目にします。 重心の作図の仕方はもちろんですが、その三角方程式の解き方 三角方程式の基本形( sinθ=c sin θ = c , cosθ= c cos θ = c , tanθ =c tan θ = c ) に式を変形して解く. aθ−b =t a θ − b = t と変数を変換することにより基本形にする.このとき,変数の変域も変換しなければならない. 例えば, sinθ sin θ




初中方程组价格 初中方程组图片 星期三




1 5三角形邊上高的直線方程式 Youtube
高校数Ⅱ「図形と方程式」。 三角形の面積。 さて、今回は、座標平面上の三角形の面積の求め方です。 例えば、こんな問題。 問題 点O (0,0)、B (8,2)、C (3,5)を頂点とする三角形OABの面積を求めよ。 これも、実際に座標平面にこの三角形を描いて考えると 基本三角方程式では、三角比の値から角度を求める問題を考えました。ここでは、三角比の相互関係も使った、より方程式っぽい問題を考えることにします。 例題1 例題 $0^{>━━━━━━━━━━━━━━━━< 動画まとめシートを配布中! 《 林俊介の公式LINE




4种方法来计算三角形面积



三角爱学的方程式png搜索网 精选免抠素材 透明png图片分享下载 Pngss Com
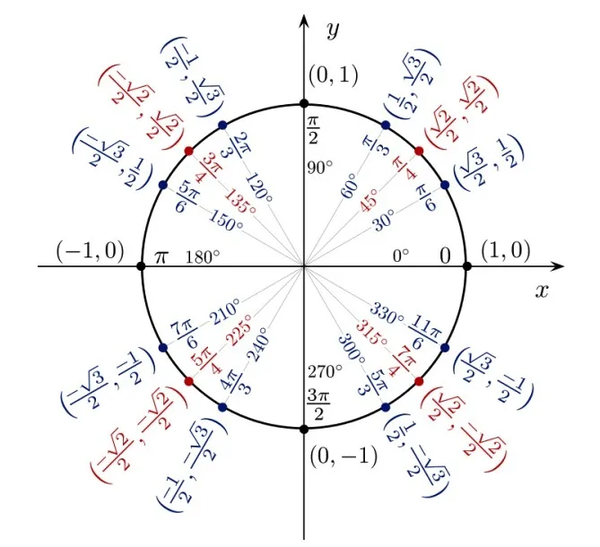
ですのでこれなら解ける形の三角関数の方程式です。単位円を考えてあげれば、 $$\theta=\frac{\pi}{6}\ ,\ \frac{5}{6}\pi\ ,\ \frac{3}{2}\pi$$ と出てきます。置き換えまで終わればあとはやったことがある形なので安心ですね。 いったん広告の時間です。 ヘロンの三角形 (723, 724, 725) を求めよう 上記のペル方程式の解から、3辺の長さが という形になるヘロンの三角形を求めていきましょう。 のとき、 です。 このとき、3辺の長さは となり、面積は となります。 たしかにヘロンの三角形になっています。高校講座HOME >> 数学Ⅱ >> 第回 第2章 図形と方程式 座標と直線の方程式 平面上の点の座標 (2) 三角形の形状・平面上の内分点 数学Ⅱ ラジオ第2




11等边三角形面积公式勾股定理初中数学初二 Youtube




平面方程 小孔明的专栏 Csdn博客 平面方程
相互関係を利用する三角方程式の解き方 三角関数の相互関係を用いて式を簡単にして,前節の置換できる形まで変形させる解法です。 相互関係は 他の公式の導出にも頻出 なので必ず覚えましょう。 三角関数の相互関係の導出について詳しく知りたい方変数分離形の微分方程式とは? 例えば \(x\) の関数 \(y\) があるとき, \(x\) , \(y\) 及び \(y\) の導関数の方程式を微分方程式と呼びました。 このうち, \(y\) の導関数が1階導関数だけの微分方程式を1階微分方程式といいます。 運動方程式 \(F = ma\) は2階導関数を含む2階微分方程式です。 三角不等式1 のとき、次の不等式を満たす θ の値の範囲を求めよ。 先ほどは方程式を扱いましたが、今度は不等式です。 境界値だけでなく「どちら側か」にも注目します。 正接 (tan) の場合は、定義域にも注意しましょう。 上図において、半円弧のうち




三角形摩尔浓度公式计算 三角形png图片素材免费下载 图片编号 Png素材网



方程式 万图壁纸网
三角形の内心と傍心の軌跡について 軌跡の方程式の導出法と軌跡の存在領域 龍谷大学理工学部 大西 俊弘(Toshihiro Onishi) 四 \grave{}ノ\grave{} 谷 晶二 (Shoji Yotsutani) 山岸 義和 (Yoshikazu Yamagishi) Faculty of Science and Technology, Ryukoku University 図形と方程式|2点間の距離と三角形の形状について 今回は、2点間の距離と三角形の形状について学習しましょう。 平面上の2点間の距離は、図形の辺の長さに応用されます。 2点間の距離から、座標平面上にある図形の辺の長さを知り、その結果、図形の 化学方程式的一个小三角形是加热符号。 表示的是加热的意思。 加热是指热源将热能传给较冷物体而使其变热的过程。 一般的外在表现为温度的升高,可以用温度计等设备直接测量。 加热的方式一般可分为直接加热和间接加热两大类。 例如碳酸氢钠受热
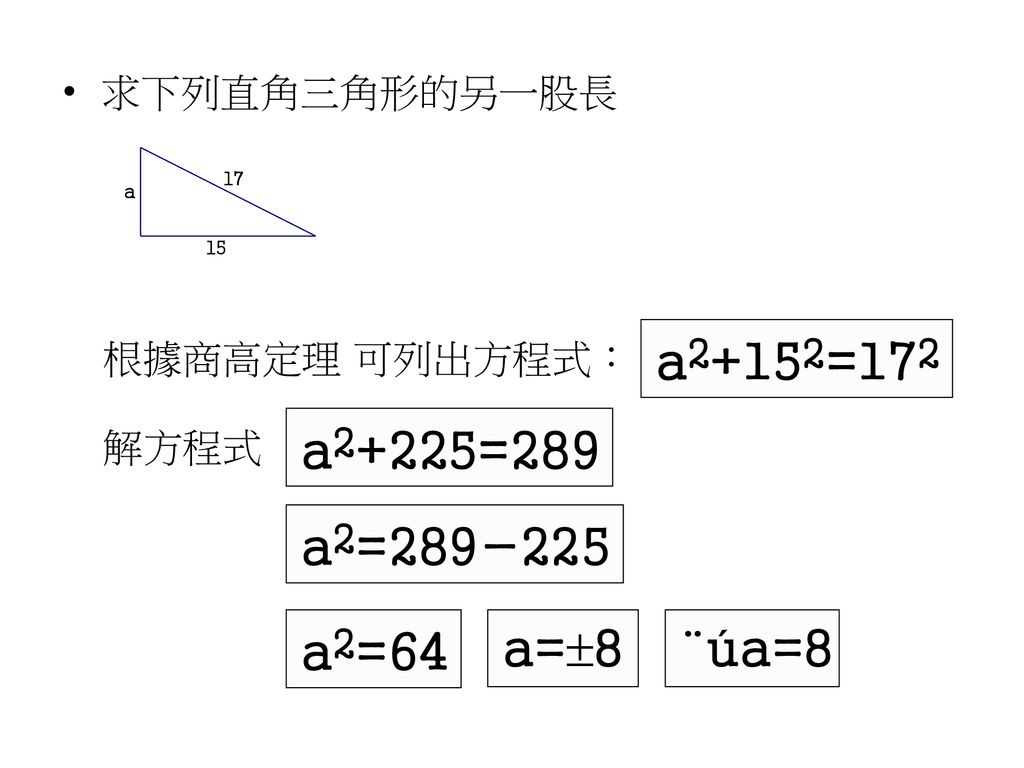



有一個長方形 它的長是6公分 寬是8公分 問它的對角線長是多少公分 Ppt Download




如何通过三角形的顶点坐标找到边的方程 数学21
三角比を含む方程式sin 三角比を含む方程式cos 三角比を含む方程式tan 練習問題に挑戦! まとめ! 中3受験生へこの力を身につけたら本番で60点は楽勝にとれる! こちらの関連記事はいかがでしょうか? この形でも平面の方程式を表せているので答えになっています。 a x b y c z d = 0 axbyczd=0 a x b y cz d = 0 の形に直したいときには連立方程式を解いて s , t s,t s , t を消去しないといけないので少しめんどうです。この表にない値,例えば のどれも「筆算では」解けません.解けるのは,この表にある の場合だけです. 中学校で習う1次方程式の解き方 など違って, を「数式変形で」解く方法はありません. のような問題は「教科書の巻末に付いている三角関数表を見て」解くのです.




数学公式 绿色学校黑板数学公式 手写科学数学方程式理论向量例证 插画包括有选件类 图画



三角手绘类方程式免抠素材免费下载 觅元素51yuansu Com
求角と方程式 角度を求めることは、小学生のころにもやっていることです。 しかし、角度を求めるために方程式を用いることは中学生ならではです。 そんな問題を練習しましょう。 例題1 次の図の角 \(x\) の大きさを求めなさだから、この性質を持つ三角形を知っていたいと、思っていました。 ここで、特に、3辺の長さが連続する3つの自然数の場合を考えます。 問題1: x 2 =3y 2 +1(一つのペル方程式) である、負でない整数解(x、y)を求めてください。 一部の特殊解でも三角形面積の2倍値detAを用いる。 (3)Bマトリックス 節点の変位より歪(ひずみ)を算出する係数である。その係数値を 算出する式は、歪の定義式に形状関数の代入にて得られる。 (4)Dマトリックス 節点の変位より応力を算出する係数である。



用solidworks方程式建模的正三角環 修改參數後圖形會自動變化 雪花新闻
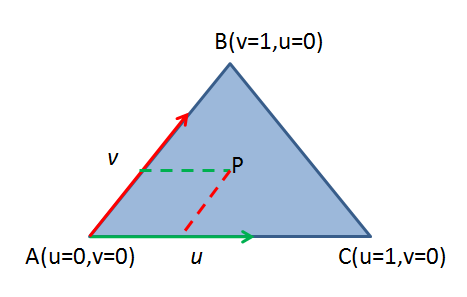



求解射线与三角形交点的算法 Jack Huang S Blog




三角形中的直线方程 参考网




Watlow 三角形和y 型电路方程式



干货分享 三角形中的直线方程 中线 高 角分线




如何通过三角形的顶点坐标找到边的方程 数学21




3 1 平面方程式




傲览千古on Twitter 描述曲线和曲面的代数方程式描述实心直角三角面描述直角三角形描述阴空心直角三角面




勞厄方程式 维基百科 自由的百科全书



三角爱学的方程式免抠素材免费下载 觅元素51yuansu Com



初中数学 利用相似三角形 构造一元二次方程式 网易视频



数学方程式草稿纸学习元素素材下载 正版素材 摄图网



测试金字塔的奥秘和数学 技术圈



泵的基本方程式 三联泵业股份有限公司




3种方法来求直角三角形斜边的长度



1




改变世界的17个方程式 每一个都是天才的设计 网易订阅



Ch1 直線方程式 1 5 1 6 我的m讚




在pages中使用方程式时 如何使平方根不那么 高 21




三角的数学方程式png图片素材免费下载 图片编号yrkenbdq Pngbag素材网




翻轉學習影片 高中 數學 三角形邊上高的直線方程式



聯立方程式的圖形例題講解 三直線圍成三角形 直角坐標與二元一次方程式的圖形 七下 發現學習的美麗新世界




数学ii 図形と方程式 2 2 三角形の形状 Youtube




利用双曲线的特征三角形解高考题 知乎



初中数学方程式大全你需要的公式都在这里 初三网




高考数学多解篇 6种方法求三角形面积最值 技巧性强 每日头条



4一元二次的解 腾讯视频




空间射线与三角形相交算法的两种实现 Globalizationa的博客 Csdn博客
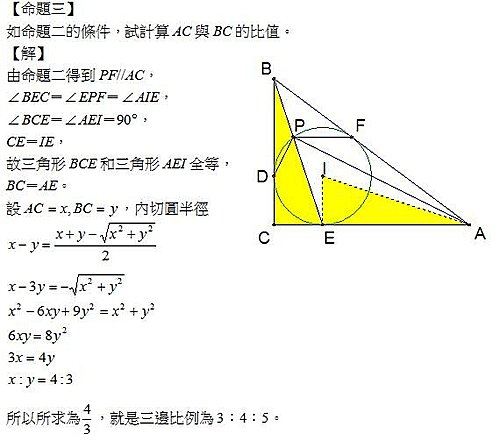



345直角三角形的性質 老王的夢田 痞客邦



数学三角形图片免费下载 数学三角形素材 数学三角形模板 新图网



圆的方程式 万图壁纸网



数学矢量无缝模式与手写的数学公式 计算 方程式 您可以使用任何颜色的背景库存矢量图 免版税




二丁8號高毅哲直線方程式




确定斜边的长度 建议 August 21



展示数学美丽和力量的11个方程式 你最喜欢哪一个 快资讯



ようこそアンパンの部屋へ 三角形の面積や長さの公式




三角形 21 直角三角形面積的基本計算題 Youtube




科学史上最美丽最重要的9个数学方程式 哔哩哔哩




常用的放大器配置设计方程式 讨论 放大器专区 Engineerzone



三角爱学的方程式png搜索网 精选免抠素材 透明png图片分享下载 Pngss Com




方程式 方程式图片 方程式素材下载 稿定素材



1



数学老师喊麦三角函数刷屏 Sat数学三角函数了解一下 知乎



初中数学 直角三角形中 利用中点和勾股定理 构造方程式求解 哔哩哔哩 Bilibili



一例子关于解决一方程式和num 一变化的总数关于指已提到的人我插画 正版商用图片30gxcu 摄图新视界



中2 数学 08 いろいろな連立方程式 In 数学中2 On Vimeo




3种方法来计算三角形的周长



手绘数学矢量无缝图案 手写代数公式 方程式和几何图形在白皮书上库存矢量图 免版税



改变世界的方程式




长方形手绘类方程式png图片素材免费下载 图片编号qpwkwvgy Pngbag素材网



中考数学等边三角形和分式方程结合的压轴难题秒杀解题技巧分享 哔哩哔哩 つロ干杯 Bilibili



用solidworks方程式建模的正三角環 修改參數後圖形會自動變化 雪花新闻




Watlow 3 相三角形 Y 型计算器



梯形怎么画4个三角形 搜狗图片搜索




工作三角形公式幂方程科学公式png图片素材免费下载 图片编号 Png素材网




數學一點也不無聊 數學遊戲 誰偷喝了老師的牛奶 搭配單元 三角形的三心 方程式的圖形 相似形 直角坐標平面




一元一次方程 新人首单立减十元 21年8月 淘宝海外




如何用斜率判斷是不是直角3角形 Clear



2次方程式 三角形と動点の文章問題 勉強ナビゲーター



物理動畫 數學 等差數列 1




傲览千古on Twitter 如果是在 平面拓扑几何学 中 该方程式 X Y R 可描述多种不同的曲线 即使它们是那种 不同胚 的一维曲线 比如 它可描述一条直线段 或者一个圆 或者一个直角三角形



干货分享 三角形中的直线方程 中线 高 角分线



二氧化碳三角转化图 氮三角转化图及方程式 化学三角转化大全



求解射线与三角形交点的算法 Jack Huang S Blog



怎么求正方形的方程式 百度经验




一个小三角形表示 化学方程式的一个小三角形是什么意思 三人行教育网 Www 3rxing Org




例題 一元二次應用題 直角三角形 Youtube




3d打印教学模型 展现数学方程式之美 知乎




高二數學空間中的平面方程式 急 信欣茗數學園地 隨意窩xuite日誌



三角的数学方程式矢量图png图片免费下载 素材7xsqgawju 新图网



怎么求正方形的方程式 百度经验




外接圓 维基百科 自由的百科全书




双摆运动三角形方程png图片素材免费下载 图片编号 Png素材网



直角三角形 维基百科 自由的百科全书



Q Tbn And9gcq Hqeajhkitlcwnwlppuyepcnpxetx5choj5msbtvfox8yjkaz Usqp Cau




中一年級試卷和答案17 Pdf




Amazon Com 教養方程式 你的角色 決定孩子如何出色 Traditional Chinese Edition Ebook 隆納 弗格森 Ronald F Ferguson 塔莎 羅伯森 Tatsha Robertson 王素蓮 Kindle Store




Watlow 三角形和y 型电路方程式



用solidworks画一个八字圈 要用到3d草图和方程式驱动的曲线 轮廓



名師課輔網 直線平分三角形面積求方程式
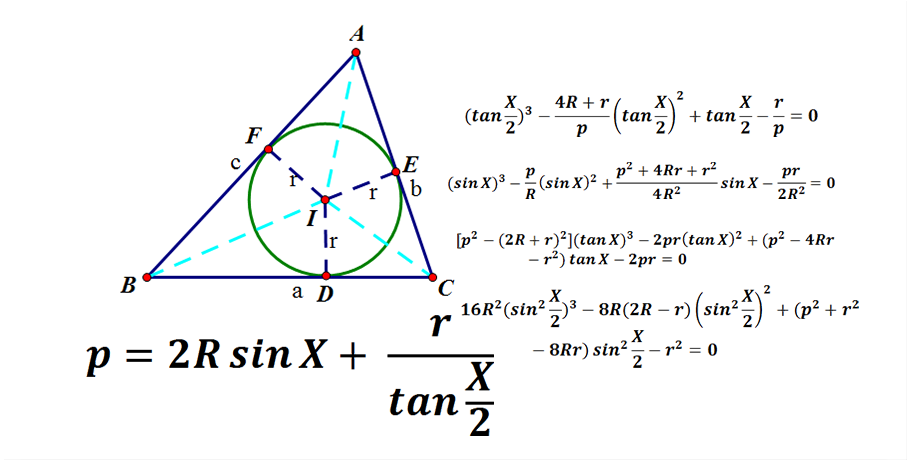



三角形与一元三次方程 知乎




直線方程式



1



正三角形外接圆算法 西瓜视频搜索
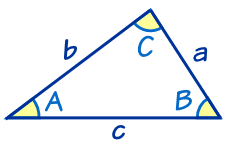



解三角形



名師課輔網 直線方程式及圖形 等腰三角形內心




一个统治世界的方程式 改变你对这个世界的看法




直角三角形的邊長計算公式 國中的時候 數學課教我們如果一個三角形有一個直角 夾出這個直角的兩邊長度如果分別 By Anthony Liu Medium




高校数学 三角形の内接円の方程式 受験の月



启智学术等边三角形方程式 东奇庚 新浪博客



Ae模板数学代数方程式计算公式标识揭示math Formulas Logo Reveal V2 柚皮cg资源网站




S 5 上學期考試 Q42 直線方程 三角形面積 Youtube



0 件のコメント:
コメントを投稿